Time management is very much important in IIT JAM. The eduncle test series for IIT JAM Mathematical Statistics helped me a lot in this portion. I am very thankful to the test series I bought from eduncle.
Nilanjan Bhowmick AIR 3, CSIR NET (Earth Science)
Debanjana Adhikari posted an Question
- CSIR NET
- Physical Sciences
How do we understand that three components of angular momentum not constant of motion? any short process??
The Lagrangian of a system moving in three dimensions is L=m m( si) + The independent constants of motion is/are (a) energy alone (b) only energy, one component of the linear momentum and one component of the angular momentumn (c) only energy, one component of the linear momentum (d) only energy, one component of the angular momentum
- 0 Likes
- 7 Comments
- 0 Shares
-
![comment-profile-img]() >
>
-
![comment-profile-img]() >
>
-
![comment-profile-img]() >
>
-
![comment-profile-img]() >
>
Ruby negi
you know there is no need to do calculation in this question, see here is no cyclic coordinate so no linear momentum is conserved, and lagrangian is independent of time so only energy is conserved....
-
![comment-profile-img]() >
>
-
![comment-profile-img]() >
>
Dhairya sharma
if T means time is not present in Lagrangian then it's symmetric in time . and symmetry in time leads to conservation of energy.
Do You Want Better RANK in Your Exam?
Start Your Preparations with Eduncle’s FREE Study Material
- Updated Syllabus, Paper Pattern & Full Exam Details
- Sample Theory of Most Important Topic
- Model Test Paper with Detailed Solutions
- Last 5 Years Question Papers & Answers
Sign Up to Download FREE Study Material Worth Rs. 500/-










 >
>
 >
>




 >
>
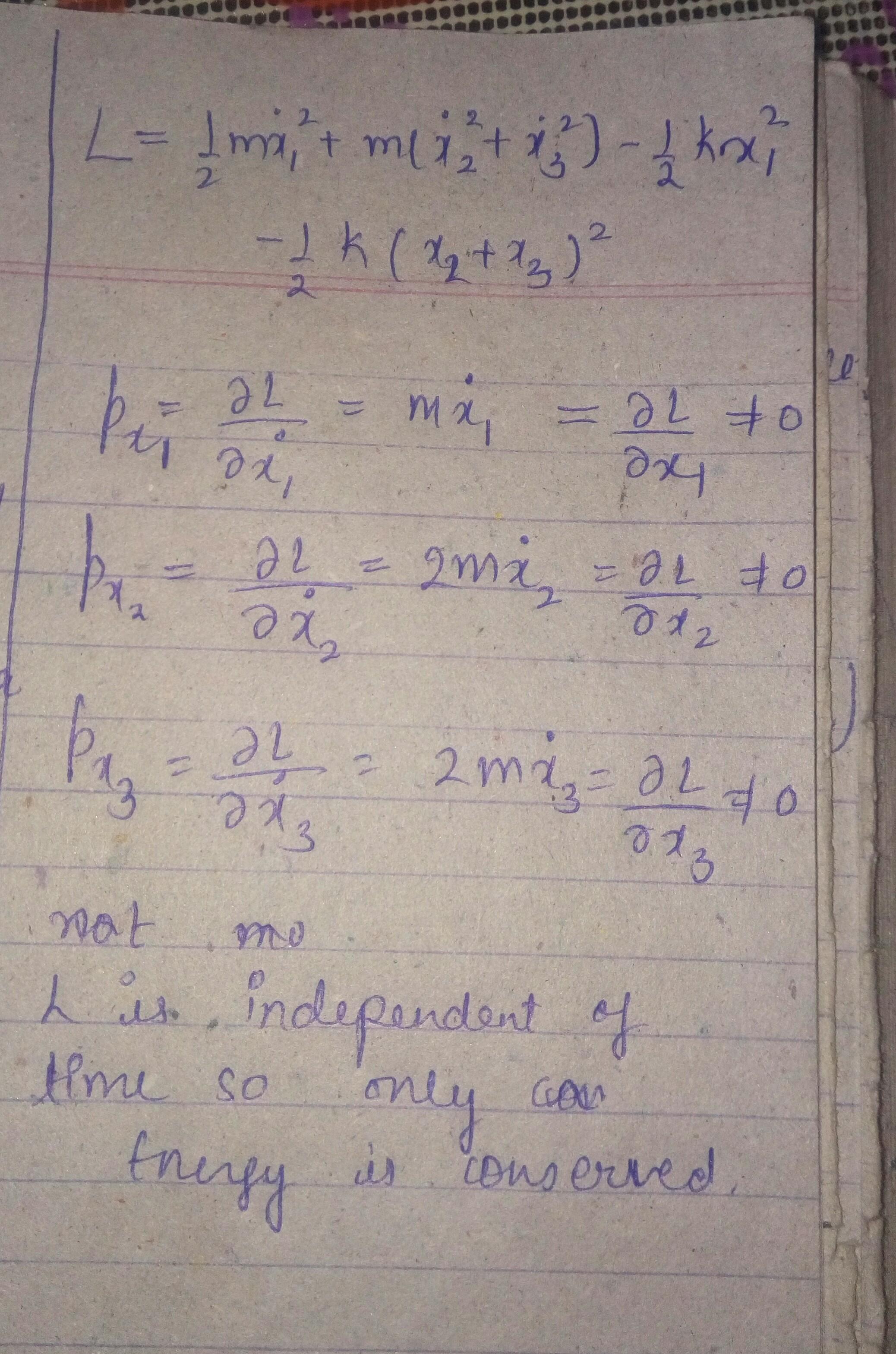
 >
>







Dhairya sharma
when something is missing in Lagrangian like x or thitha then corresponding momentum is conserved and it's called cyclic coordinate