Time management is very much important in IIT JAM. The eduncle test series for IIT JAM Mathematical Statistics helped me a lot in this portion. I am very thankful to the test series I bought from eduncle.
Nilanjan Bhowmick AIR 3, CSIR NET (Earth Science)- IIT JAM
- Mathematics (MA)
9.1 (nat) let f: r+r be a differentiable function such that f'(a) = fr) for all ze . suppose that f[ar) ancd f(57) are two nonzero solution ot the tollowing dif
9.1 (NAT) Let f: R+R be a differentiable function such that f'(a) = fr) for all zE . Suppose that f[ar) ancd f(57) are two nonzero solution ot the tollowing differential equation ,dy rPd + 3y =0 satistying f(ar)f(3r)= f(2r) and f(or)f(-Br) = f(r) then value of p is given by Q.2 (NAT) equation lf g(r) = Ae" +e #2 be the solution of the following differential dy -6y=0 da? dr satistying 0)=5 then y(0) equals Q.3 (MCQ) Let z, I+e", 1 +r+e" be the solution of a second order linear differ- ential equation with constant coetticients. If y(r) is the solution of same differential equation satistying g(0)=3 and 0) =4 the y(1) equals (a) e+l (b) 2e+3 (c) 3e+2 (d) 3e+2 Q.4 (NAT) If y(r) is the solution of following differential equation d++4y-0 v0)-2 -0 then y(log2) equals. Q.5 (NAT) If g(r) be the solution of the following differential equation satishes y(0)=I and 0)-I then y(T) attains its maximum at
- 0 Likes
- 6 Comments
- 0 Shares
Do You Want Better RANK in Your Exam?
Start Your Preparations with Eduncle’s FREE Study Material
- Updated Syllabus, Paper Pattern & Full Exam Details
- Sample Theory of Most Important Topic
- Model Test Paper with Detailed Solutions
- Last 5 Years Question Papers & Answers
Sign Up to Download FREE Study Material Worth Rs. 500/-










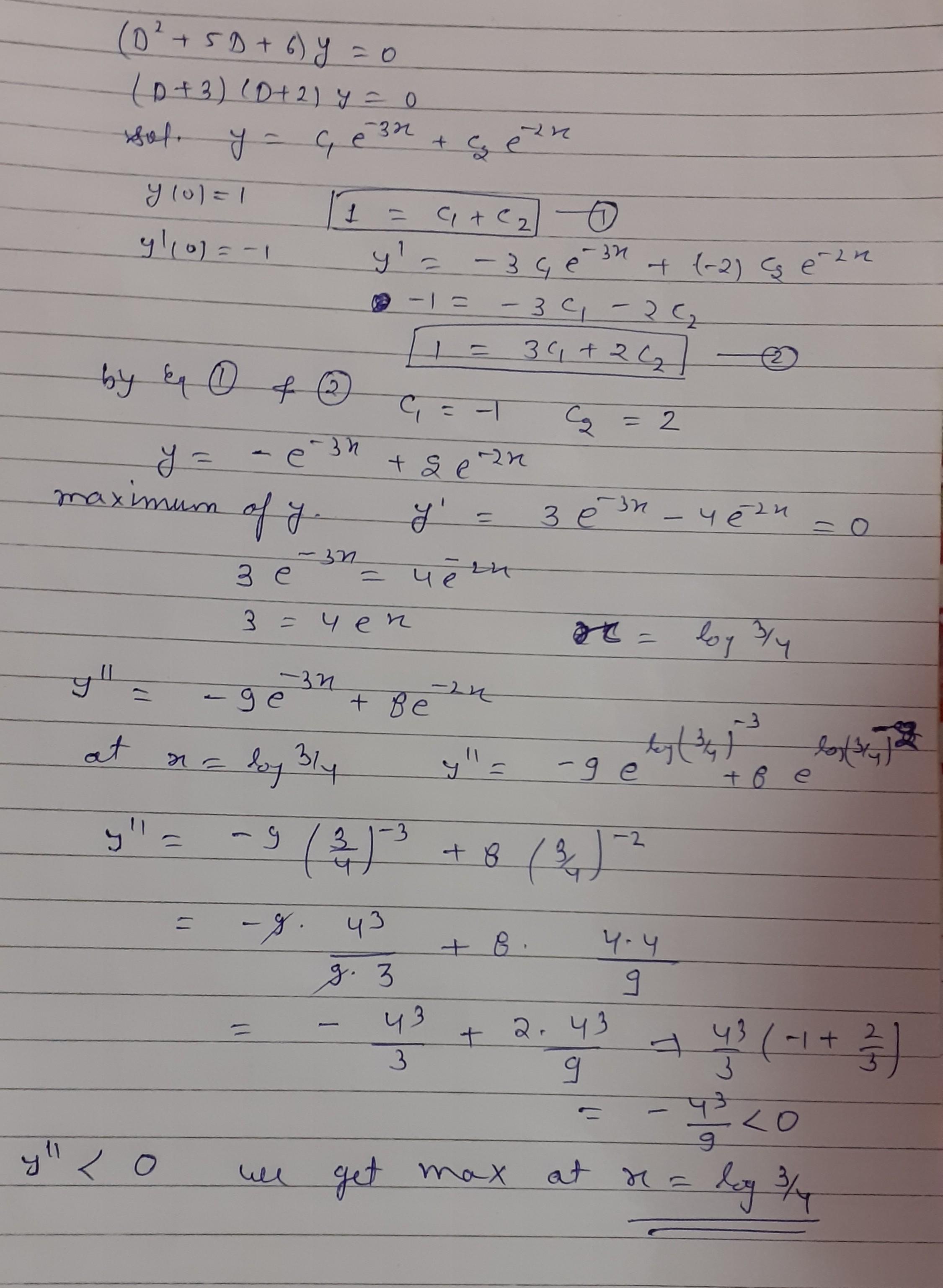
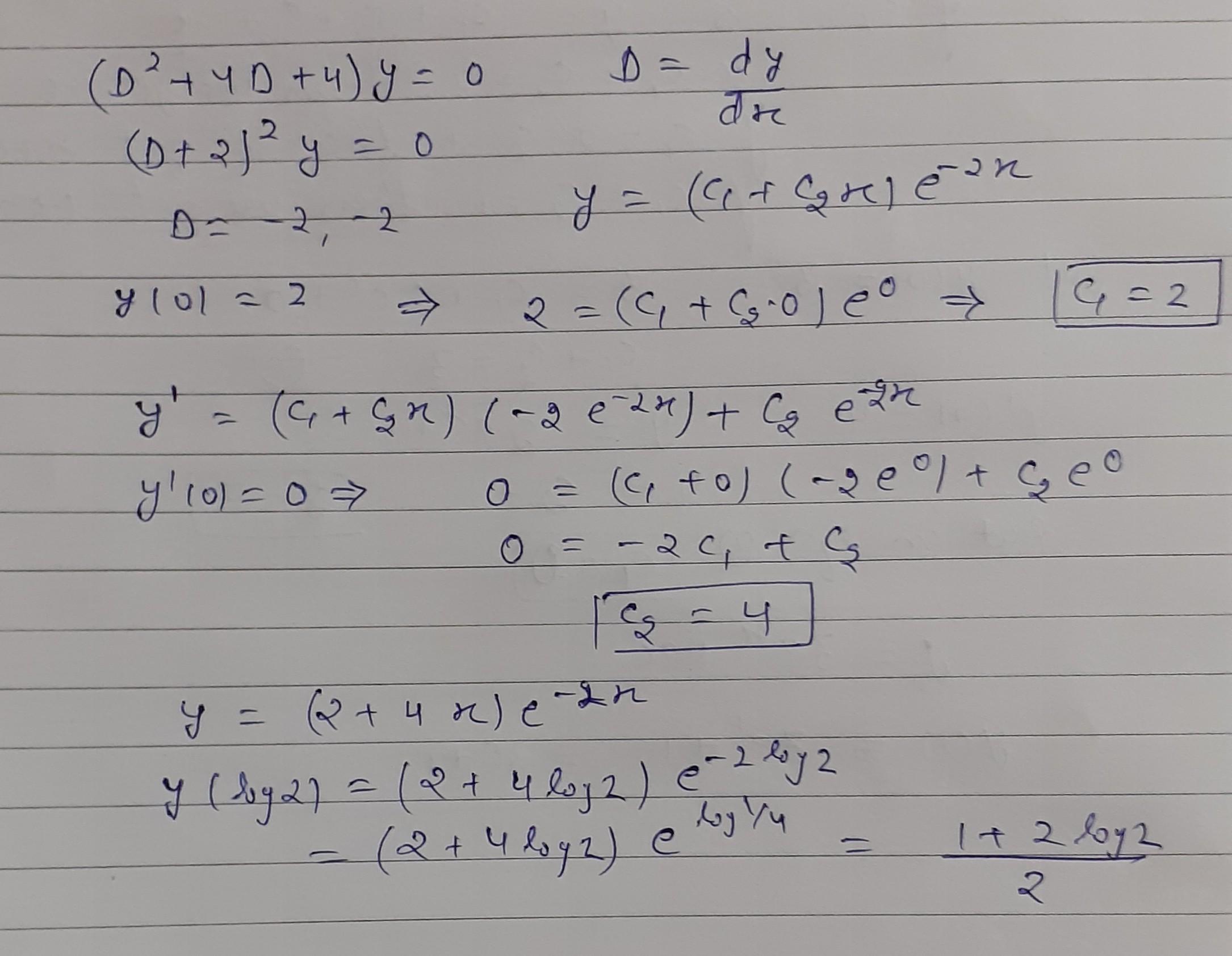


 >
>

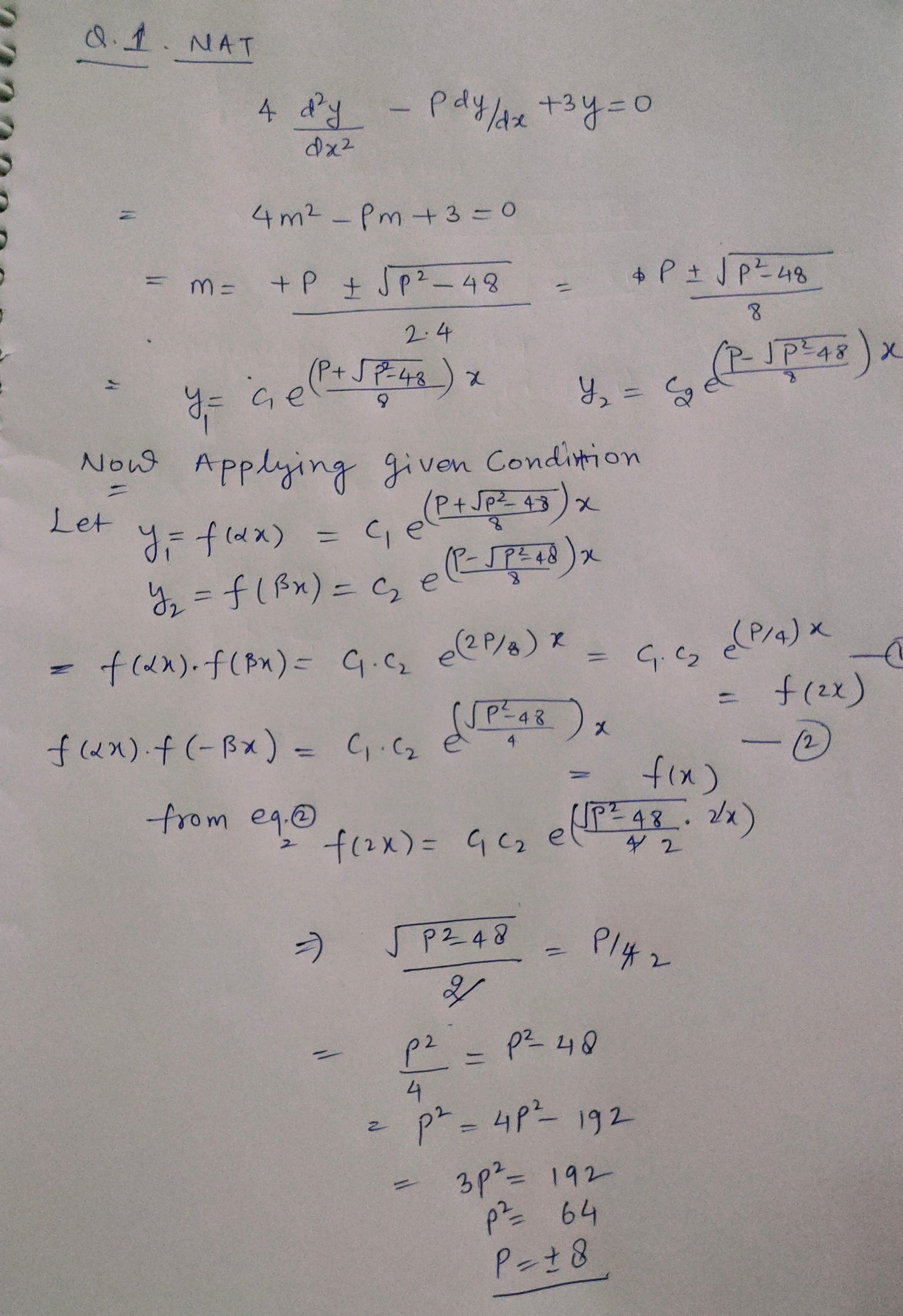







Kiran goswami![best-answer]()
Q.3 answer 3e+1 Q2 answer is 5 Q4 answer see attachment Q5 answer is log(3/4) see attachment Q1 answer is 8