Time management is very much important in IIT JAM. The eduncle test series for IIT JAM Mathematical Statistics helped me a lot in this portion. I am very thankful to the test series I bought from eduncle.
Nilanjan Bhowmick AIR 3, CSIR NET (Earth Science)- IIT JAM
- Mathematics (MA)
9 let v, = (1, 0) v, = (1, -1) and v, = (0, 1), then how many linear transformations t: rr are there such that t(v,) = v t(v) = v t(v) = v,?
9 Let v, = (1, 0) v, = (1, -1) and v, = (0, 1), then how many linear transformations T: RR are there such that T(v,) = V T(V) = V T(v) = V,?
- 1 Likes
- 8 Comments
- 0 Shares
-
![comment-profile-img]() >
>
-
Subhankar dhara
see it
-
![comment-profile-img]() >
>
Deepak singh 1
any doubt then ask
-
![comment-profile-img]() >
>
-
![comment-profile-img]() >
>
-
Shashi ranjan sinha
in case of R² into R², again there doesn't exist any such linear transformation... see the attachment
![cropped1092714304148376283.jpg]()
![eduncle-logo-app]()
but solutions is three
![eduncle-logo-app]()
are you sure that the domain is R²?.... because in that case , you can see in the above attachment that there doesn't exist any linear transformation satisfying the given conditions
![eduncle-logo-app]()
yes domain is R^2
![eduncle-logo-app]()
okk.... then in that case, go with the above which shows that if we assume T be the linear transformation satisfying the given conditions, then we will have a contradiction....hence there doesn't exist any such linear transformation
Do You Want Better RANK in Your Exam?
Start Your Preparations with Eduncle’s FREE Study Material
- Updated Syllabus, Paper Pattern & Full Exam Details
- Sample Theory of Most Important Topic
- Model Test Paper with Detailed Solutions
- Last 5 Years Question Papers & Answers
Sign Up to Download FREE Study Material Worth Rs. 500/-











 >
>
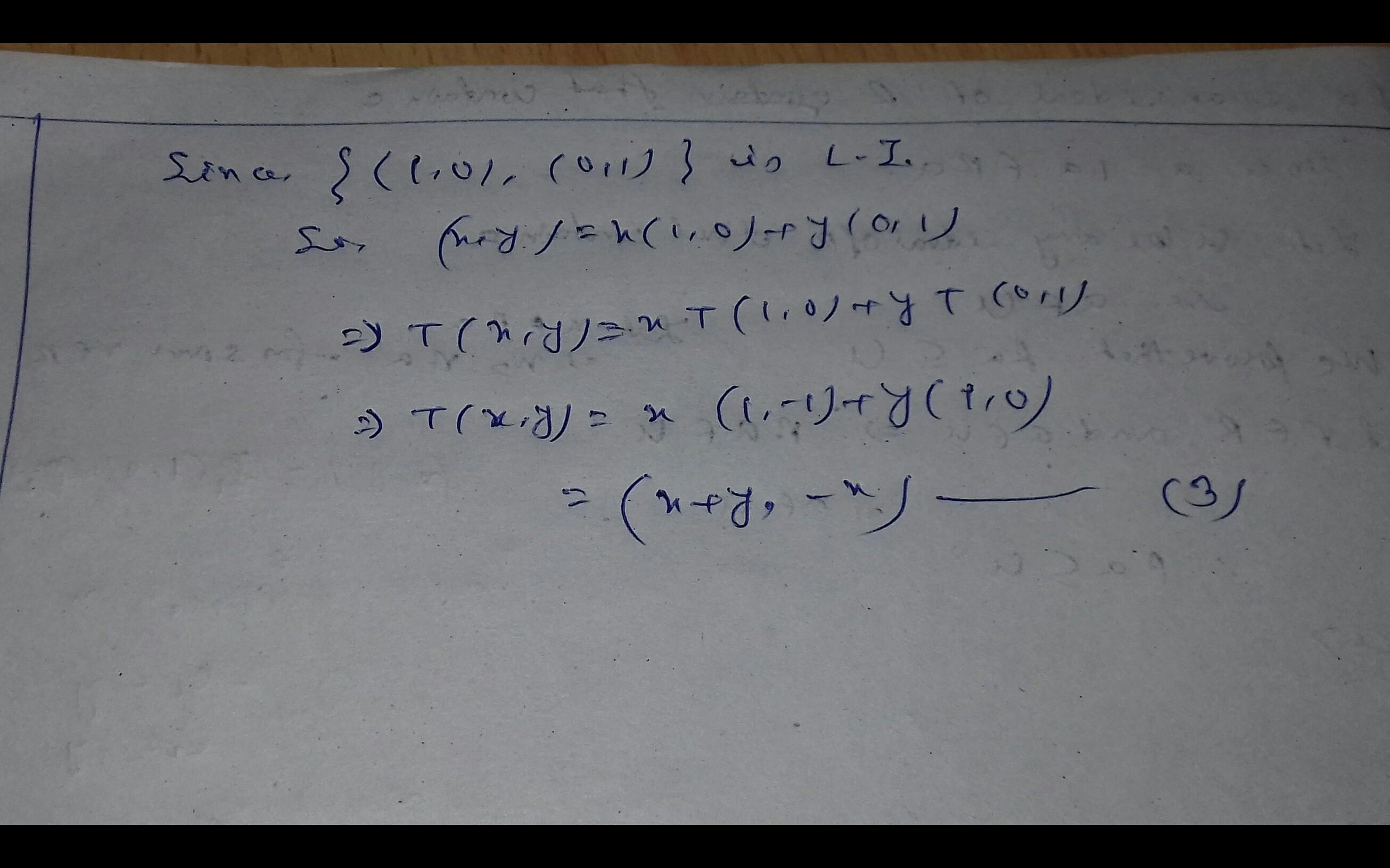

 >
>


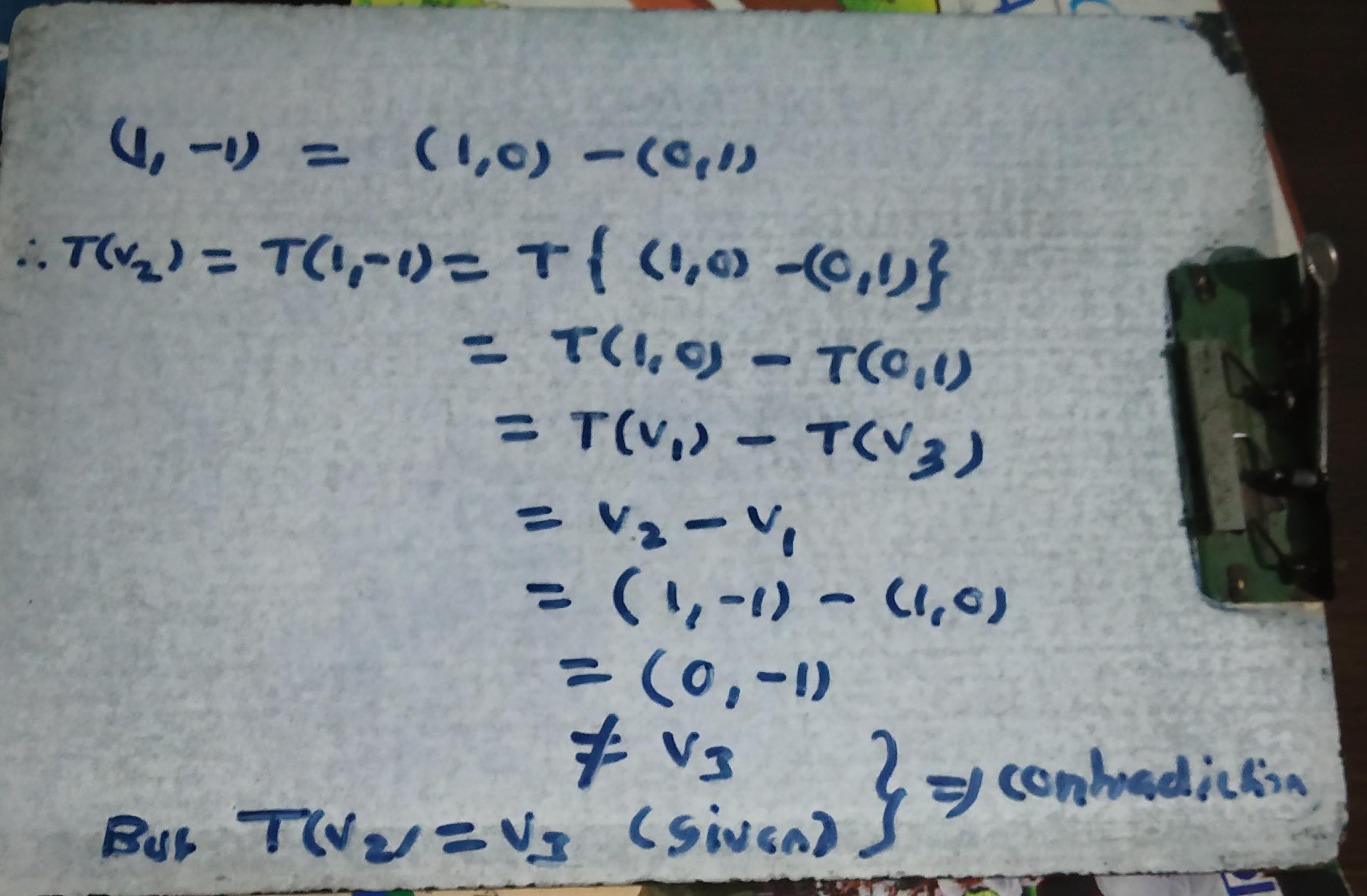








Piyush pachauri![best-answer]()
PFA
Any doubt then you can ask.