Time management is very much important in IIT JAM. The eduncle test series for IIT JAM Mathematical Statistics helped me a lot in this portion. I am very thankful to the test series I bought from eduncle.
Nilanjan Bhowmick AIR 3, CSIR NET (Earth Science)- IIT JAM
- Mathematics (MA)
A. (1) state and prove tailor's theorem with lagrange's form of remainder. log n n-i vn+1 (i) test the convergence of the infinite series 2 b. )examine if the f
a. (1) State and prove Tailor's theorem with Lagrange's form of remainder. log n n-i Vn+1 (i) Test the convergence of the infinite series 2 b. )Examine if the function xlx| is differentiable. ii) Examine, if the function fo,y) =xy x, y) + (0,0) and 0, otherwise is differentiable at the origin. C. (1) Find a reduction formula for 1, = | cos" x sin nxdx m,n being positive integers and hence deduce that 24 +. .t- m i) Findr sin xdr d. Evaltuate l} sin(x + y)dudy over R: 10S x s0 sy s R i)Evaluate J (x+ y dxdydz over R bounded by y=x, x=2, y=l. e. (i) Prove that 1/(x+y+1)' is an integrating factor of (2xy-y-y)dx + (2xy-x--x)dy=0 and find the solution of this equation. i) Solvexdy - ydx i) Find the solution of the differential equation xdx + ydy _ax-y V x+y f. dy y= ptanp +log cos p,(p =*) dx (i) Solve p(x+y)=x(x+y). (p=dy/dx)
- 0 Likes
- 4 Comments
- 0 Shares
Do You Want Better RANK in Your Exam?
Start Your Preparations with Eduncle’s FREE Study Material
- Updated Syllabus, Paper Pattern & Full Exam Details
- Sample Theory of Most Important Topic
- Model Test Paper with Detailed Solutions
- Last 5 Years Question Papers & Answers
Sign Up to Download FREE Study Material Worth Rs. 500/-










 >
>








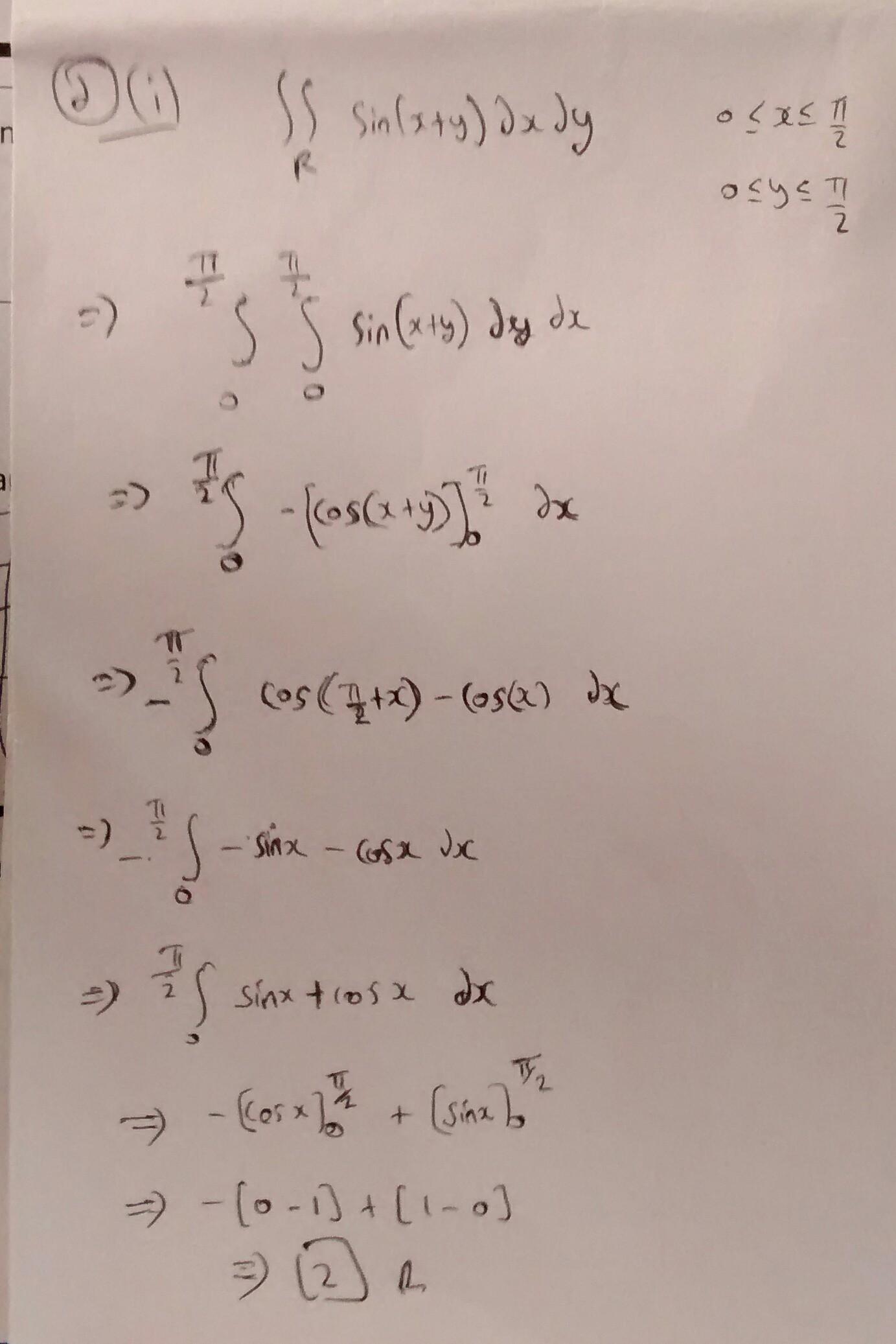
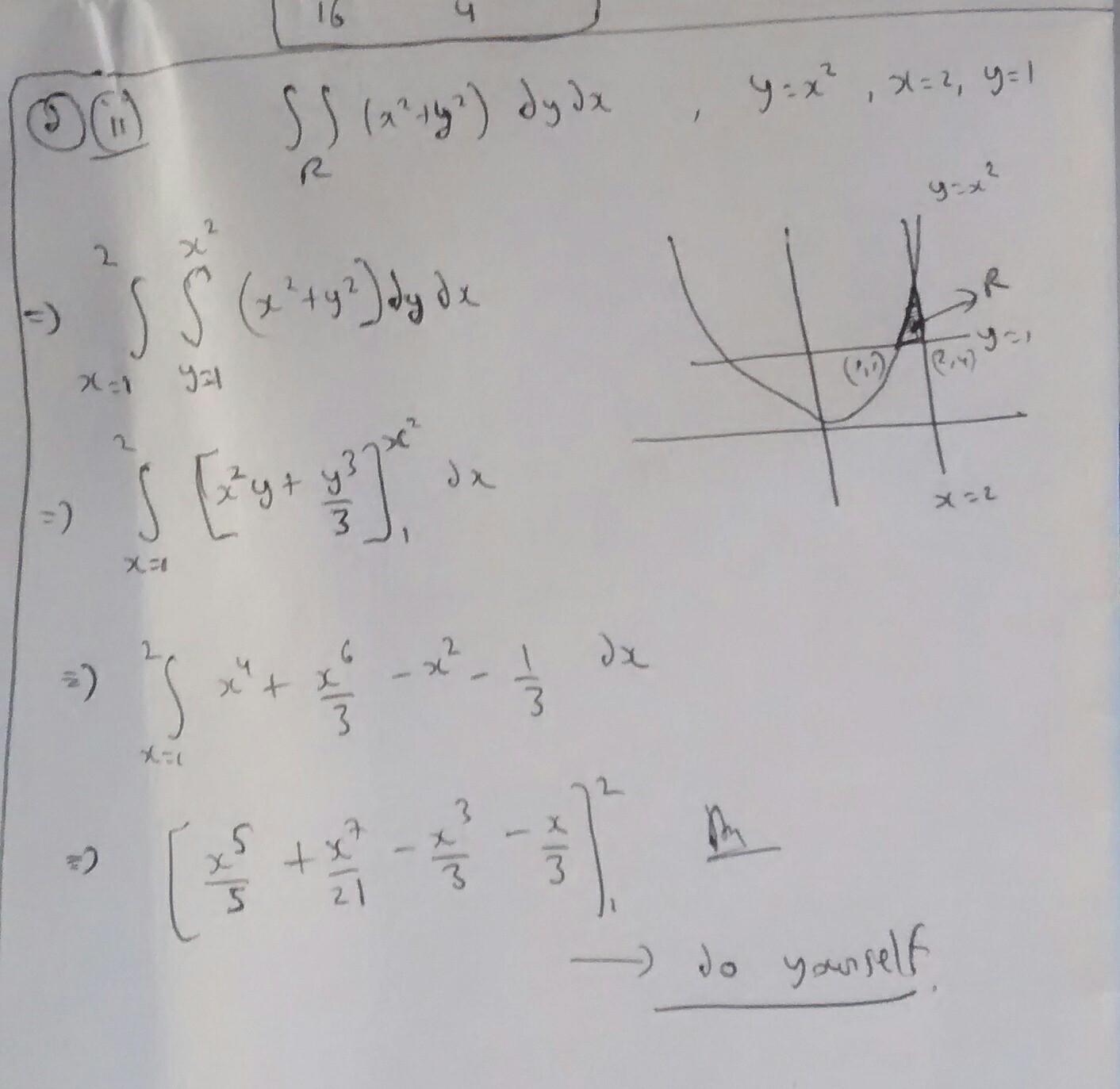







Deepak singh 1
next ..rest of question are easy u can do..