Time management is very much important in IIT JAM. The eduncle test series for IIT JAM Mathematical Statistics helped me a lot in this portion. I am very thankful to the test series I bought from eduncle.
Nilanjan Bhowmick AIR 3, CSIR NET (Earth Science)- IIT JAM
- Physics (PH)
Find the time period of the function f(t)=2cos(10t+1)-sin(4t-1)
find the time period of the function f(t)=2cos(10t+1)-sin(4t-1)
- 0 Likes
- 6 Comments
- 0 Shares
-
![comment-profile-img]() >
>
-
![comment-profile-img]() >
>
-
![comment-profile-img]() >
>
-
Udayan
why u take the LCM of those two periods
![eduncle-logo-app]()
this is the property that when you have two functions in the like addition subtraction form then the time period is equal to lcm of two two functions...
![eduncle-logo-app]()
and lcm of the fraction form is in my attached page. go through it..
![eduncle-logo-app]()
ma'am can u upload the property where's form u can know
-
![comment-profile-img]() >
>
Abhishek singh
![best-answer]()
period of first term (cos()term) is 2π/10. period of second term is 2π/4. and period of the function is LCM of these two periods.
![eduncle-logo-app]()
if you have any doubt, do let me know!
![eduncle-logo-app]()
how may I help you?
![eduncle-logo-app]()
pls describe why u take the LCM to find the the time period
![eduncle-logo-app]()
what is periodic of a function?, the smallest number which when you add to the variable and the function doesn't change. Now let say you have two functions with period 2 and 3 respectively. it means, in function F1 if you add 2 the the function wouldn't change. what if you add 4 instead of 2, then also the function won't change and similarly adding 6, 8,10 will also not chnage the function. now for function F2, if you add 3, 6 , 9, then the function won't change. what is common to both the list. list1 = (2,4,6,8,...) and list2 = (3,6,9,...). 6 is common. and you know 6 is LCM of 2 and 3.
![eduncle-logo-app]()
that's can understood ,l want to knowing why u take the LCM to find the time period
![eduncle-logo-app]()
i just give the demonstration that you have to take LCM to fulfill the definition of period of a function.
![eduncle-logo-app]()
but can u explain that the time period of a function which is the adding of two another function is the LCM of those two functions's time period
![eduncle-logo-app]()
I can't explain better than this. You sould read the question again, then read my explanation. if you got it, it would be best. other than that, I don't think a better explanation even exist.
![eduncle-logo-app]()
is there no proof that the time period of f() is the LCM of two other functions time period
Do You Want Better RANK in Your Exam?
Start Your Preparations with Eduncle’s FREE Study Material
- Updated Syllabus, Paper Pattern & Full Exam Details
- Sample Theory of Most Important Topic
- Model Test Paper with Detailed Solutions
- Last 5 Years Question Papers & Answers
Sign Up to Download FREE Study Material Worth Rs. 500/-










 >
>
 >
>




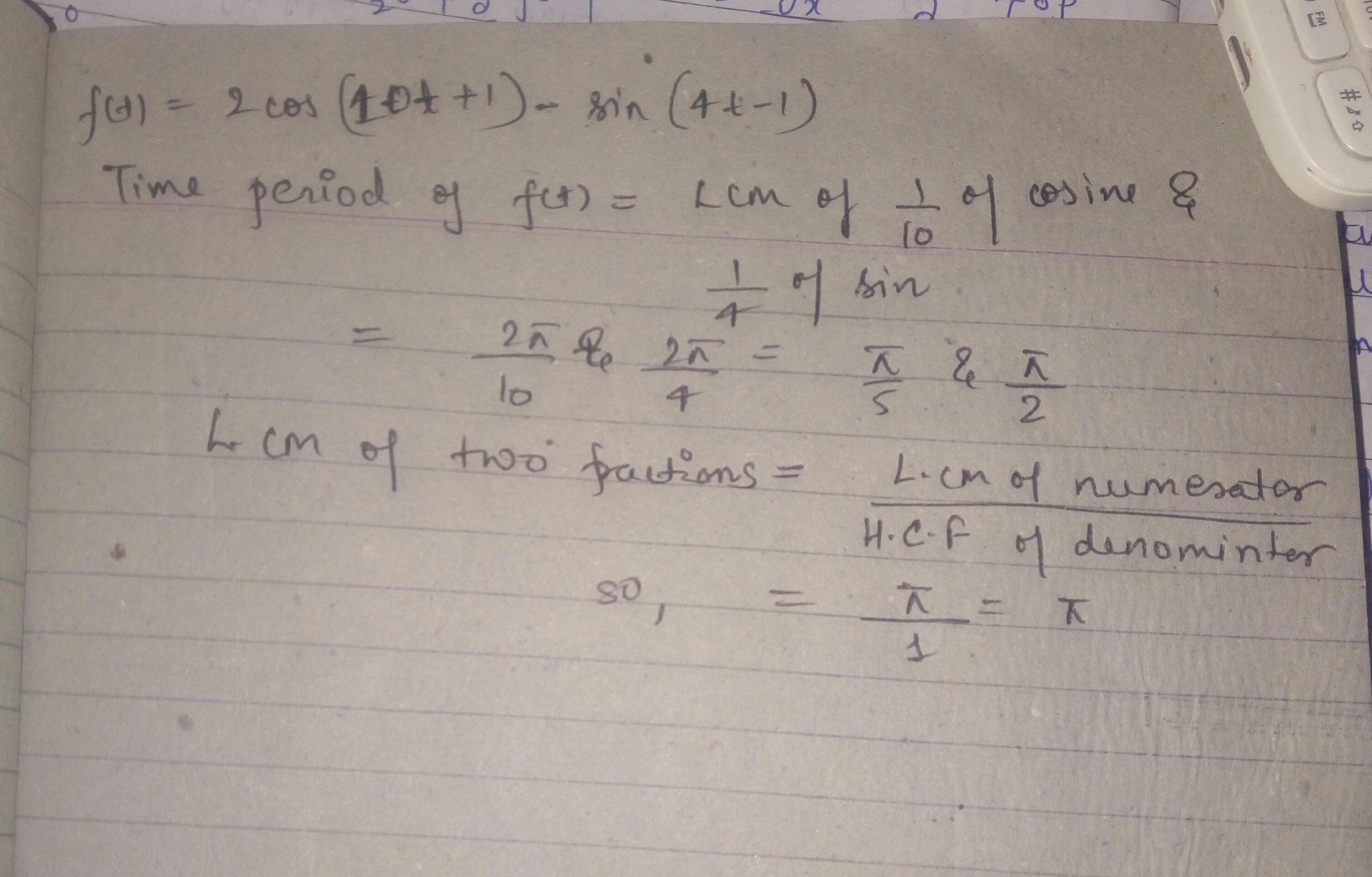
 >
>







Ujjawal vishal
see following explanation for your doubt,it may help u