30 points
>
>
>
Time management is very much important in IIT JAM. The eduncle test series for IIT JAM Mathematical Statistics helped me a lot in this portion. I am very thankful to the test series I bought from eduncle.
Nilanjan Bhowmick AIR 3, CSIR NET (Earth Science)
- IIT JAM
- Physics (PH)
Given a matrix m, find the matrix cos((pi)m/6)
Given a matrix M, find the matrix cos((pi)M/6). I solved this question using diagonalizing method. But the answer is changing if I change the positions of the eigenvalues. That is if write the eigenvalues as pi/6 and pi/2. I am getting the answer which is mentioned but if I switch the position and write pi/2 and pi/6, I am getting an answer with the negative signs switched. Can someone help?
3 Answer(s)
Answer Now
- 0 Likes
- 11 Comments
- 0 Shares
-
![comment-profile-img]()
>
-
Deepanshu Chaudhary
please see.. I have done using the same method but switched the positions of eigenvalues and I'm getting different answer
![cropped1480188701.jpg]()
![eduncle-logo-app]()
I have also changed the P matrix and D matrix accordingly
![eduncle-logo-app]()
dear, determinant is -1 u took 1
![eduncle-logo-app]()
determinant of P is -1( solution: (1*-1)/√2-(1*1)/√2=-1)
![eduncle-logo-app]()
oh okay.. I got it mam.. I forgot to divide it by the determinant
![eduncle-logo-app]()
sorry for the whole confusion
-
![comment-profile-img]()
>
Ruby negi
hope u will getting me..
-
![comment-profile-img]()
>
Ruby negi
no dear, this will not happen. please note that when u change the position of eigen value then P matrix will also change.. so keep this thing then ur ans will not change.. do it once again..
![eduncle-logo-app]()
for doubt u can ask.
![eduncle-logo-app]()
mam please check my comment.. if there is any mistake please correct me
-
![comment-profile-img]()
>
-
![comment-profile-img]()
>
Ruby negi
see
![cropped-1697072182.jpg]()
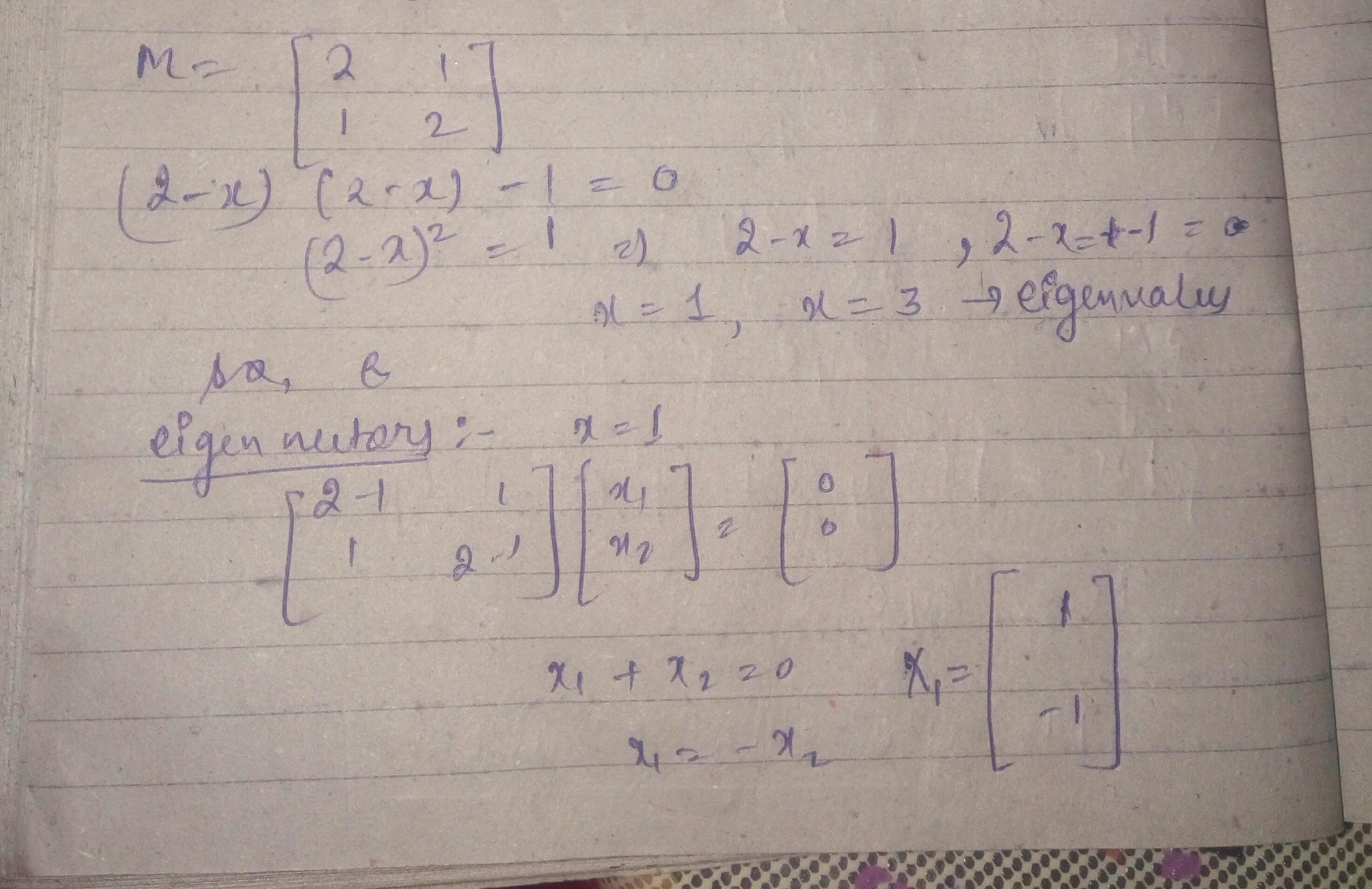
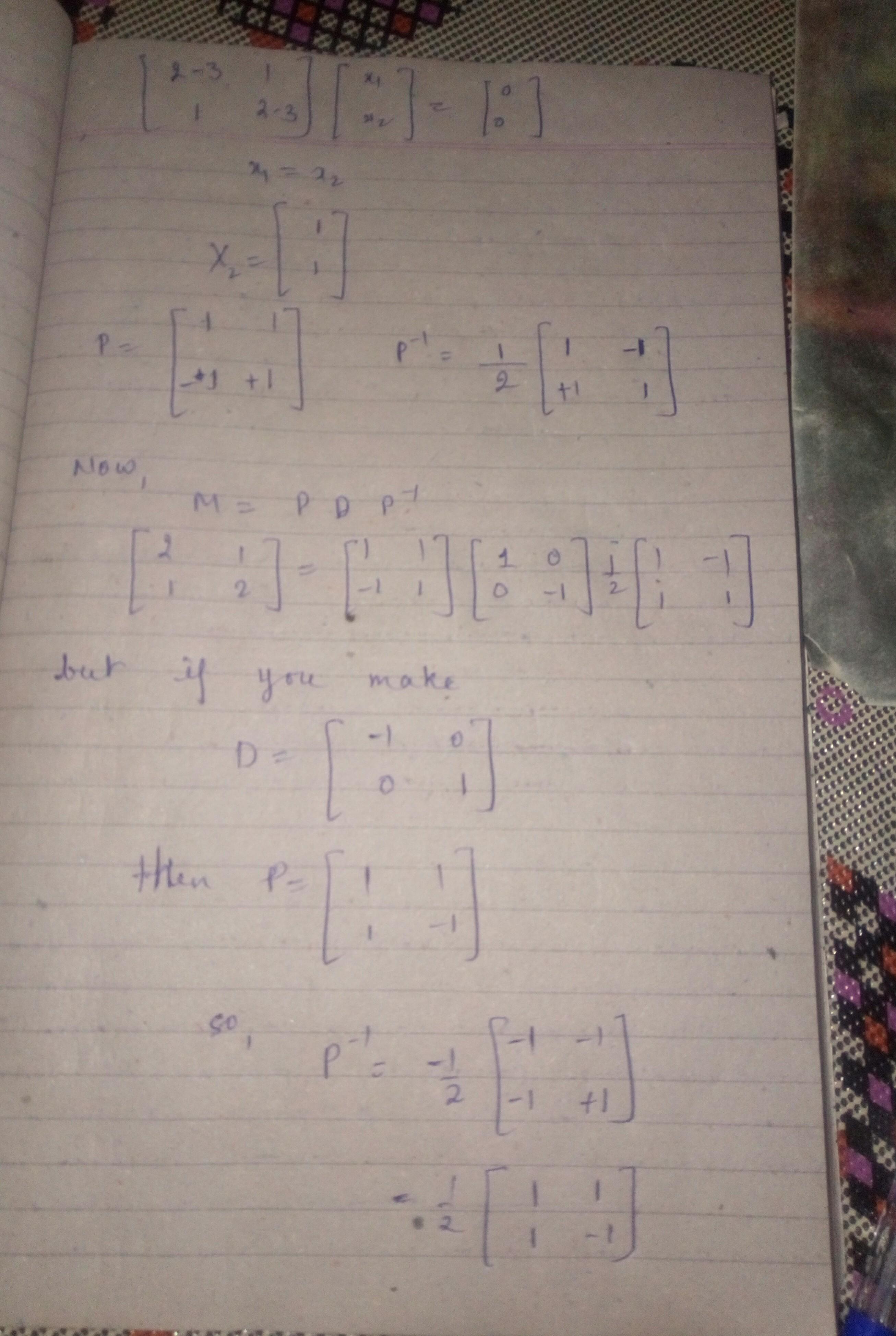
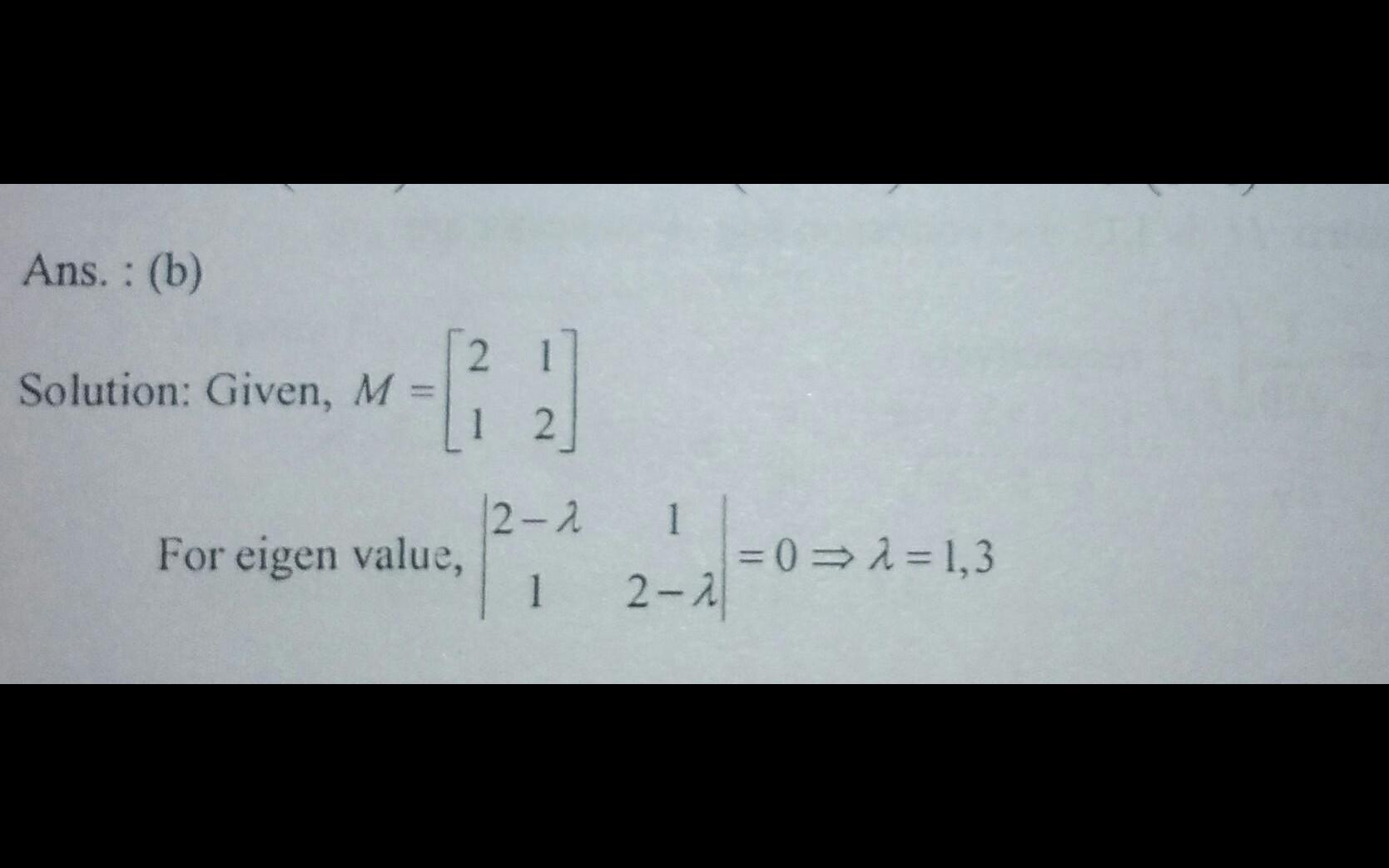
Deepanshu Chaudhary
Sorry for the whole confusion.. It was my calculation mistake
it's OK dear