IIT JAM
Harshal Asked a Question
July 26, 2020 12:03 pmpts 30 pts
  • IIT JAM
  • Mathematics (MA)

Given the matrix

  • 3 Answer(s)
Answer Now
  • 0 Likes
  • 9 Comments
  • Shares
  • Deepak singh Best Answer
    see attached, i have mentioned how to find AM and GM
    • cropped4746085130220807908.jpg
    • cropped3641614988668950878.jpg
    Likes(2) Reply(0)
  • Deepak singh thankyou
    see
    • cropped2129266006.jpg
    • cropped-436441413.jpg
    Likes(1) Reply(15)
    Harshal
    what is AM and GM?
  • Shashi ranjan sinha thankyou
    see the attachment
    • cropped1514655011480068869.jpg
    • cropped5434373778508739562.jpg
    Likes(0) Reply(9)
    Shashi ranjan sinha
    The result that I have wrote for such a matrix M is very helpful.
  • Shashi ranjan sinha
    the correct options are 1,2, 3,4
    Likes(0) Reply(3)
    Harshal
    2nd is aslo correct
  • Deepak singh
    see , it may help u
    • cropped-294417261.jpg
    Likes(2) Reply(0)
  • Deepak singh
    see, this symmetric complex matrix is no diagonizable.. so, A symmtric matrix may not be diagonizable.
    • cropped5994064840285388343.jpg
    Likes(2) Reply(0)
  • Deepak singh
    in the above example AM is not equal to GM also .. result- A matrix is diagonizable iff it has n eigenvalues and AM= GM of each eigenvalues.. this result holds in both real and...
    Show more
    Likes(2) Reply(0)
  • Shashi ranjan sinha
    Similar question has been asked in CSIR NET Dec 19 in part C
    Likes(1) Reply(0)
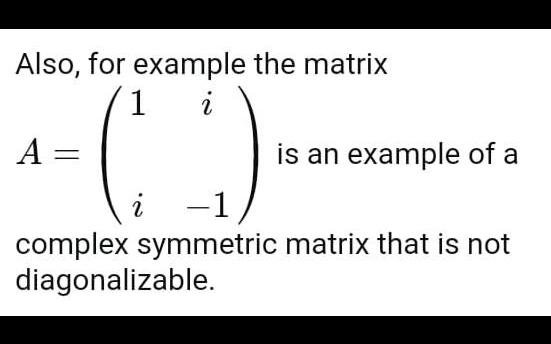
  • Deepak singh
    if any doubt then ask..
    Likes(0) Reply(0)
How Eduncle Helps You ?
StudentTutorInstitutionApp
Help
FAQsPayment TermsRefund PolicyAsk Support
Head Office :
MPA 44, 2nd floor, Rangbari main Road Mahaveer Nagar II, Kota (Raj.) - 324005

Branch Office (Jaipur):
Shyam Tower, Plot No. F2, 6th Floor Amrapali Circle,
Vaishali Nagar, Jaipur, Rajasthan 302021

Mail: info@eduncle.com
All Rights Reserved © Eduncle.com