IIT JAM
   Top Resources
profile-img
Vanshika posted an Question
July 28, 2020 • 15:50 pm 30 points
  • IIT JAM
  • Physics (PH)

How this a cos @ came here in place of z ....in sec last step as underlined??

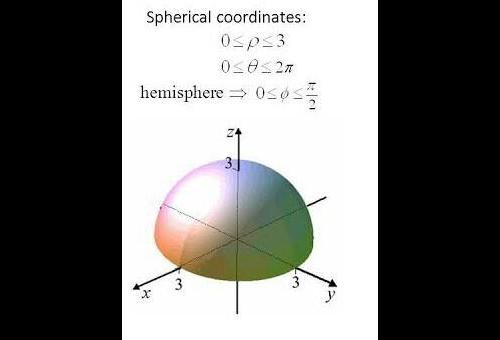
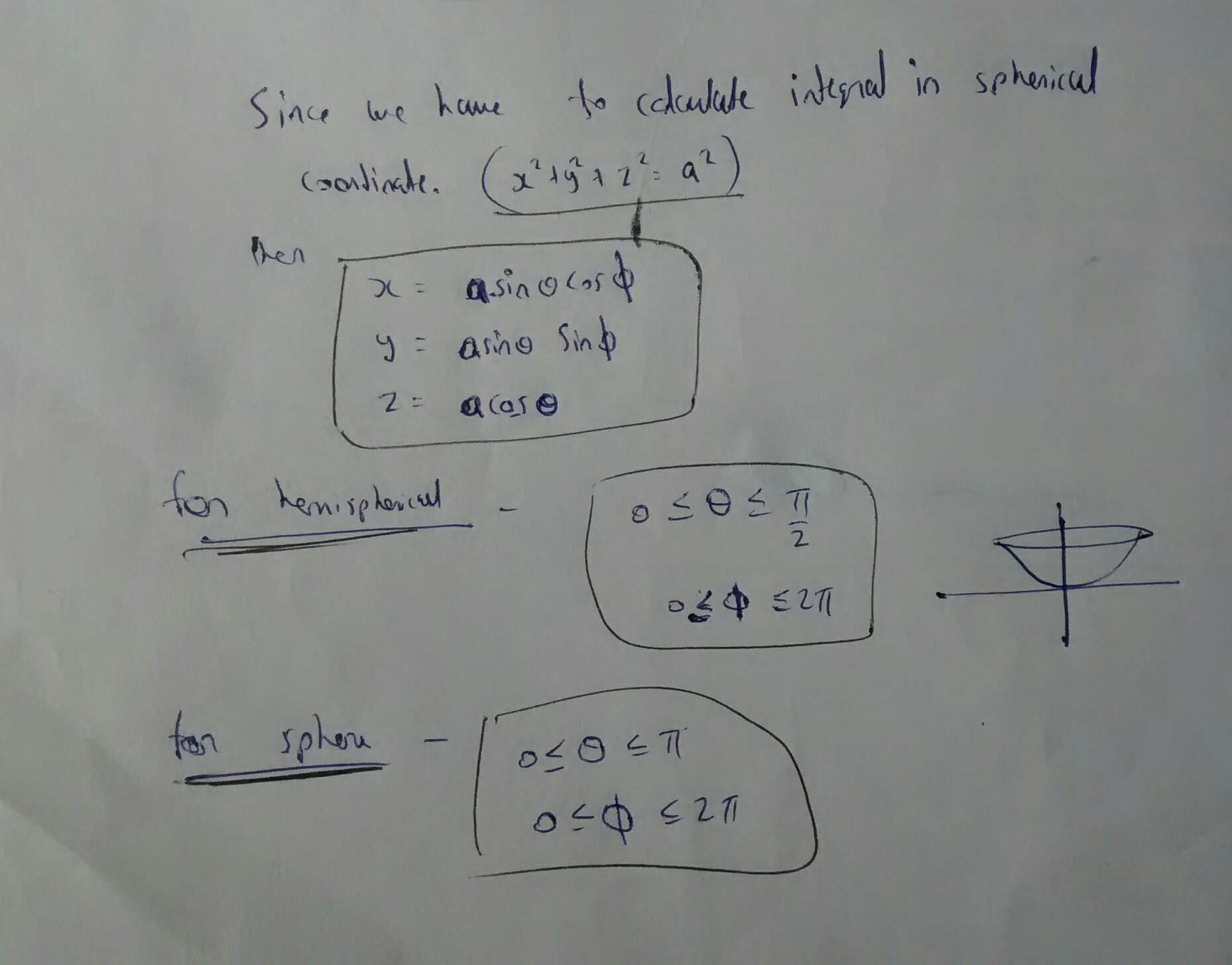
0 =k(1-4) -3k x X ay 0z (B) Here Vx V= 4y 0 2z Since the surface is a sphere with centre at the origin, f is its normal, then n1a a ix ix +jy +kz (V xv) h3k3 a a We want to evaluated-3(z/a) do over the hemisphere, In spherical coordirs 2n n/2 aCos a sin 0 de do-3a d a cos.o a sin 0 cos 0 do -0 0-0 A =- 3a2.2t. -3rma

3 Answer(s) Answer Now
  • 0 Likes
  • 5 Comments
  • 0 Shares
  • comment-profile-img>
    Ghost.

    Because they convert Cartesian coordinate to spherical coordinate system and transformation is z=radius*cos(ø). wishes

  • comment-profile-img>
    Deepak singh 1 Best Answer

    see attached

    cropped896655595.jpg
    eduncle-logo-app

    that's why we have put z = acosthta

    eduncle-logo-app

    here we have to calculate in hemispherical , that's why theta belongs to (0,pi/2) and phi belongs to (0,2pi)

    eduncle-logo-app

    any doubt then ask... it's all spherical coordinate system

    eduncle-logo-app

    thanks ...that was just slip of my mind i forgot all the little things and asking silly question .... means a lot sir 😃😃

    eduncle-logo-app

    welcome

  • comment-profile-img>
    Ravi prakash yadav best-answer

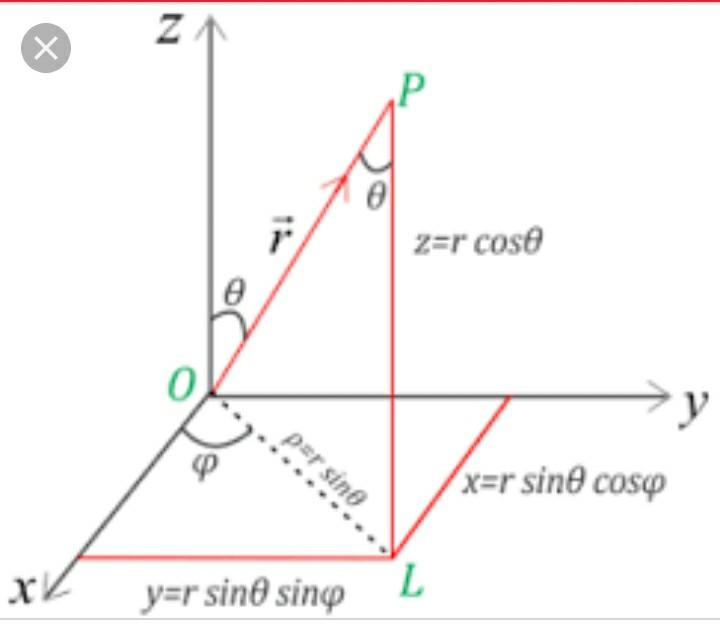
    in spherical coordinate z=acos(theta) and da=a^2sin(theta)d(theta)d(phi). we simply put z=acos(theta) and da=a^2sin(theta)d(theta)d(phi) in original equation

whatsapp-btn

Do You Want Better RANK in Your Exam?

Start Your Preparations with Eduncle’s FREE Study Material

  • Updated Syllabus, Paper Pattern & Full Exam Details
  • Sample Theory of Most Important Topic
  • Model Test Paper with Detailed Solutions
  • Last 5 Years Question Papers & Answers

Sign Up to Download FREE Study Material Worth Rs. 500/-