Time management is very much important in IIT JAM. The eduncle test series for IIT JAM Mathematical Statistics helped me a lot in this portion. I am very thankful to the test series I bought from eduncle.
Nilanjan Bhowmick AIR 3, CSIR NET (Earth Science)- IIT JAM
- Mathematics (MA)
If ah is a coset in g, then | point o a must belong to ah o a can't belong to ha o a can't belong to ah o a must belong to ah but not in ha cycles (12 3) and (1
If aH is a coset in G, then | point O a must belong to aH O a can't belong to Ha O a can't belong to aH O a must belong to aH but not in Ha Cycles (12 3) and (13 2) of S_3 1 point are S3 Inverses of each other O odd permutation Otranspositions O none of these
- 1 Likes
- 6 Comments
- 0 Shares
-
![comment-profile-img]() >
>
Deepak singh 1
![best-answer]()
in first question - a always belongs to aH ( by property of coset ) , so option i is true . and in second question- order of (123) and (132) are 3 , so can't be transposition , are even permutations and are self inverse of each other (see attachment) , So option a is correct. if any doubt then ask
![cropped3195940336644132688.jpg]()
-
![comment-profile-img]() >
>
Piyush pachauri
a must belong to aH , as H is a subgroup implies identity belongs to H , so a.e = a belong to aH Inverse of each other.
-
![comment-profile-img]() >
>
Piyush pachauri
a must belong to aH , as H is a subgroup implies identity belongs to H , so a.e = a belong to aH Inverse of each other.
-
![comment-profile-img]() >
>
Piyush pachauri
a must belong to aH , as H is a subgroup implies identity belongs to H , so a.e = a belong to aH Inverse of each other.
-
![comment-profile-img]() >
>
Do You Want Better RANK in Your Exam?
Start Your Preparations with Eduncle’s FREE Study Material
- Updated Syllabus, Paper Pattern & Full Exam Details
- Sample Theory of Most Important Topic
- Model Test Paper with Detailed Solutions
- Last 5 Years Question Papers & Answers
Sign Up to Download FREE Study Material Worth Rs. 500/-











 >
>

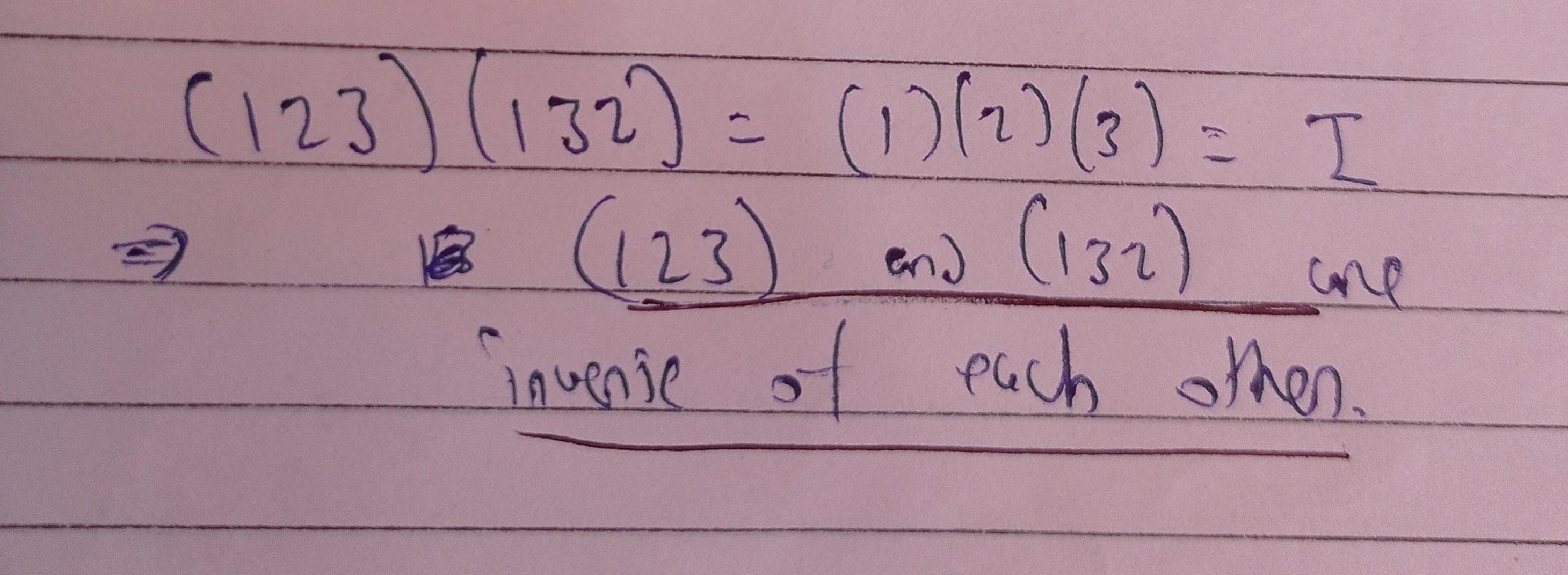
 >
>








Supriya shiwani
a must belong to aH and second qestion inverse of each other