Time management is very much important in IIT JAM. The eduncle test series for IIT JAM Mathematical Statistics helped me a lot in this portion. I am very thankful to the test series I bought from eduncle.
Nilanjan Bhowmick AIR 3, CSIR NET (Earth Science)- IIT JAM
- Mathematics (MA)
Ker(o) = {16 30 let g be a gmup and h be a cyclic group and o be a group homomorphism from g onto h, then d-h) = g is 24. abeliar: group (b) (d) (a) not abelian
Ker(o) = {16 30 Let G be a gmup and H be a cyclic group and o be a group homomorphism from G onto H, then D-H) = G is 24. Abeliar: Group (B) (D) (A) Not Abelian (C) Cyclic none of these Contac Lfe
- 0 Likes
- 4 Comments
- 0 Shares
-
Anonymous User
c because under onto homomorphism cyclic and abelian property is preserved...or we can say that onto homomorphism map cyclic group to cyclic or abelian to abelian
Do You Want Better RANK in Your Exam?
Start Your Preparations with Eduncle’s FREE Study Material
- Updated Syllabus, Paper Pattern & Full Exam Details
- Sample Theory of Most Important Topic
- Model Test Paper with Detailed Solutions
- Last 5 Years Question Papers & Answers
Sign Up to Download FREE Study Material Worth Rs. 500/-











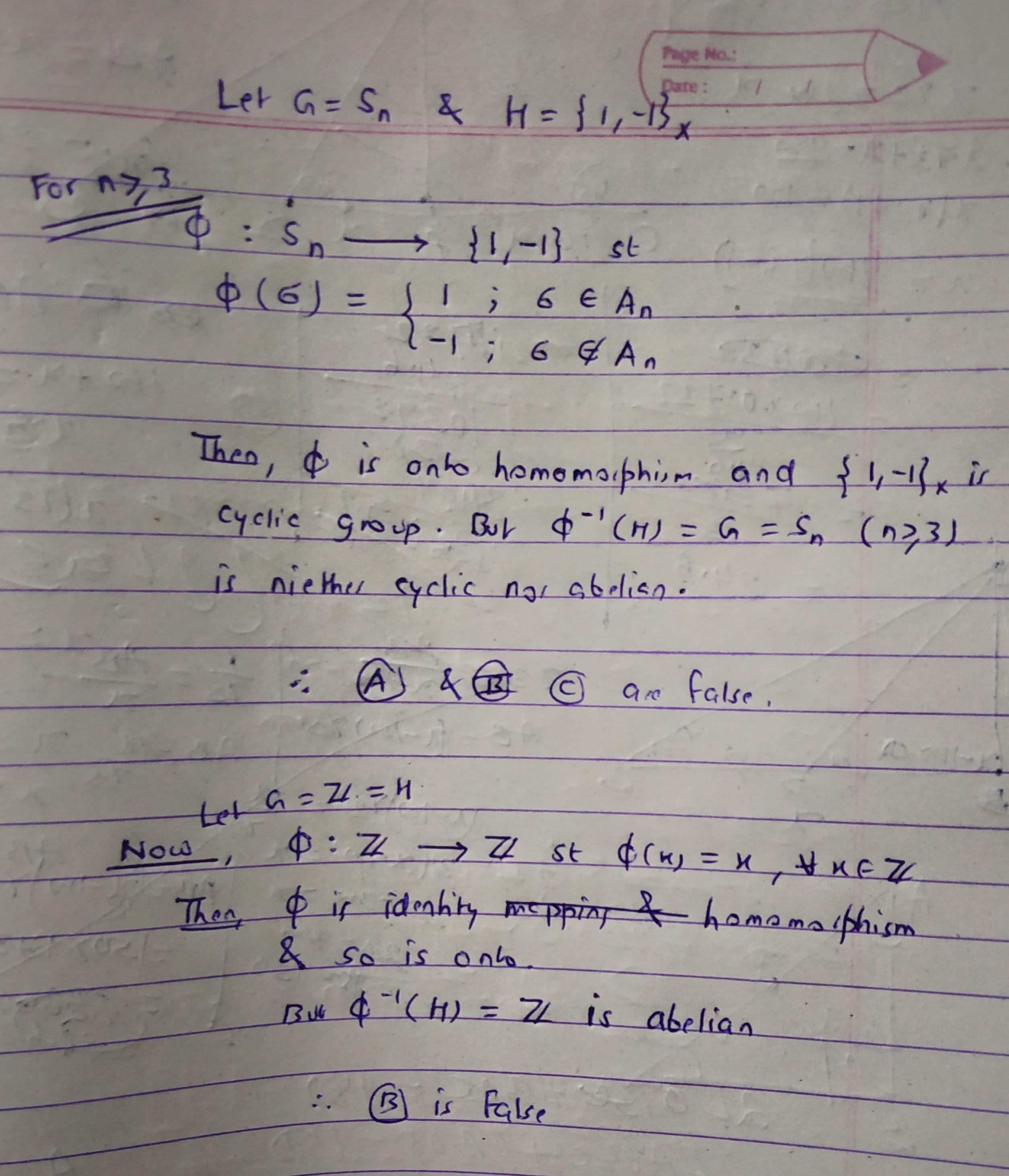








Shashi ranjan sinha
correct option is d