Time management is very much important in IIT JAM. The eduncle test series for IIT JAM Mathematical Statistics helped me a lot in this portion. I am very thankful to the test series I bought from eduncle.
Nilanjan Bhowmick AIR 3, CSIR NET (Earth Science)- IIT JAM
- Mathematics (MA)
Let v be a vector space and t transformation from v to v, then the intersection of the range af t and the null space of t is the zero subspace of v if and only
Let V be a vector space and T transformation from V to V, then the intersection of the range af T and the null space of T is the zero subspace of V if and only if. (A) range of T is different from the nullity of T (B) T)= 0x =0 (C) T(T(X) = 0 x = 0 (D) T(T(X) = 0 T(X) = 0
- 0 Likes
- 2 Comments
- 0 Shares
Do You Want Better RANK in Your Exam?
Start Your Preparations with Eduncle’s FREE Study Material
- Updated Syllabus, Paper Pattern & Full Exam Details
- Sample Theory of Most Important Topic
- Model Test Paper with Detailed Solutions
- Last 5 Years Question Papers & Answers
Sign Up to Download FREE Study Material Worth Rs. 500/-











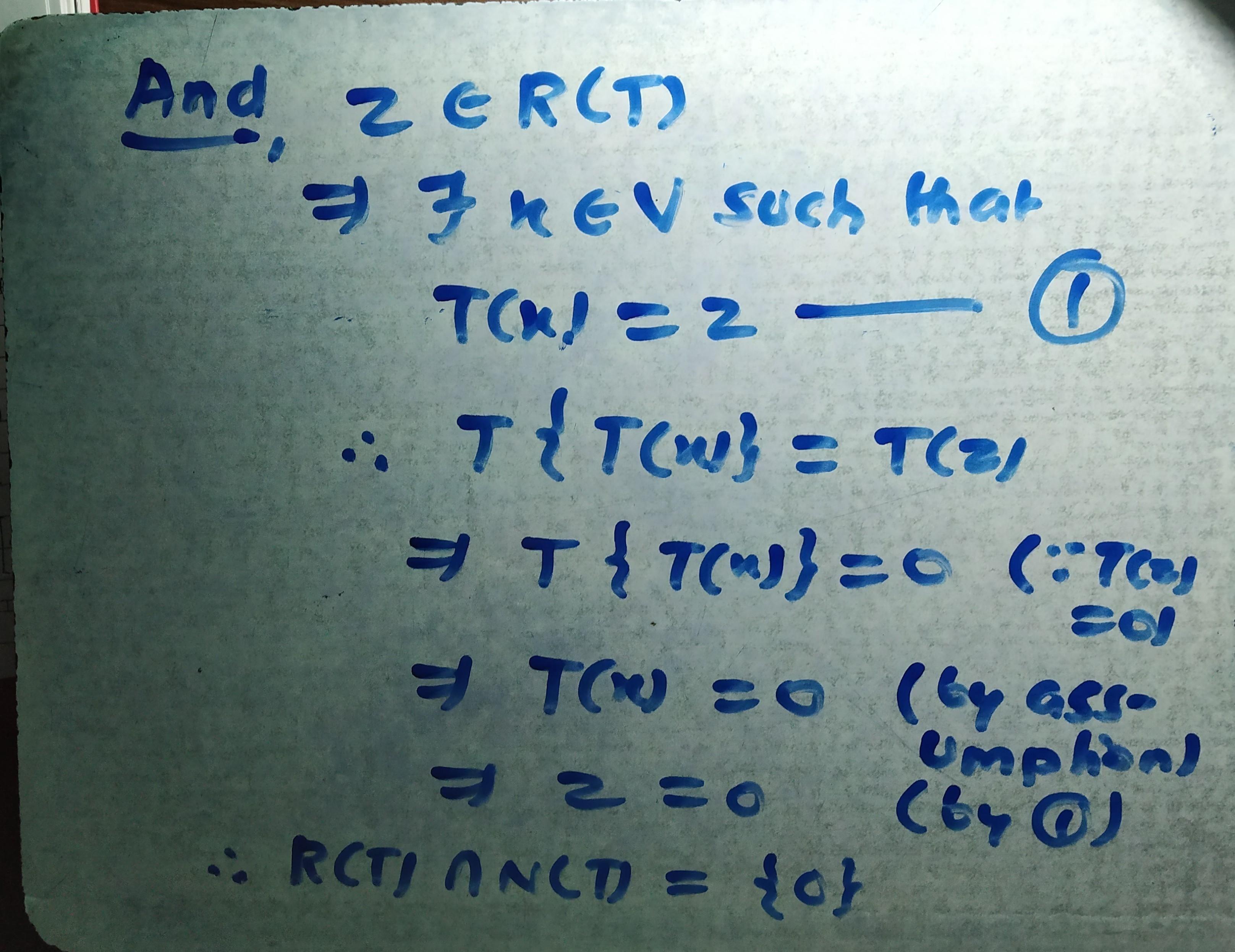








Shashi ranjan sinha
correct option is d