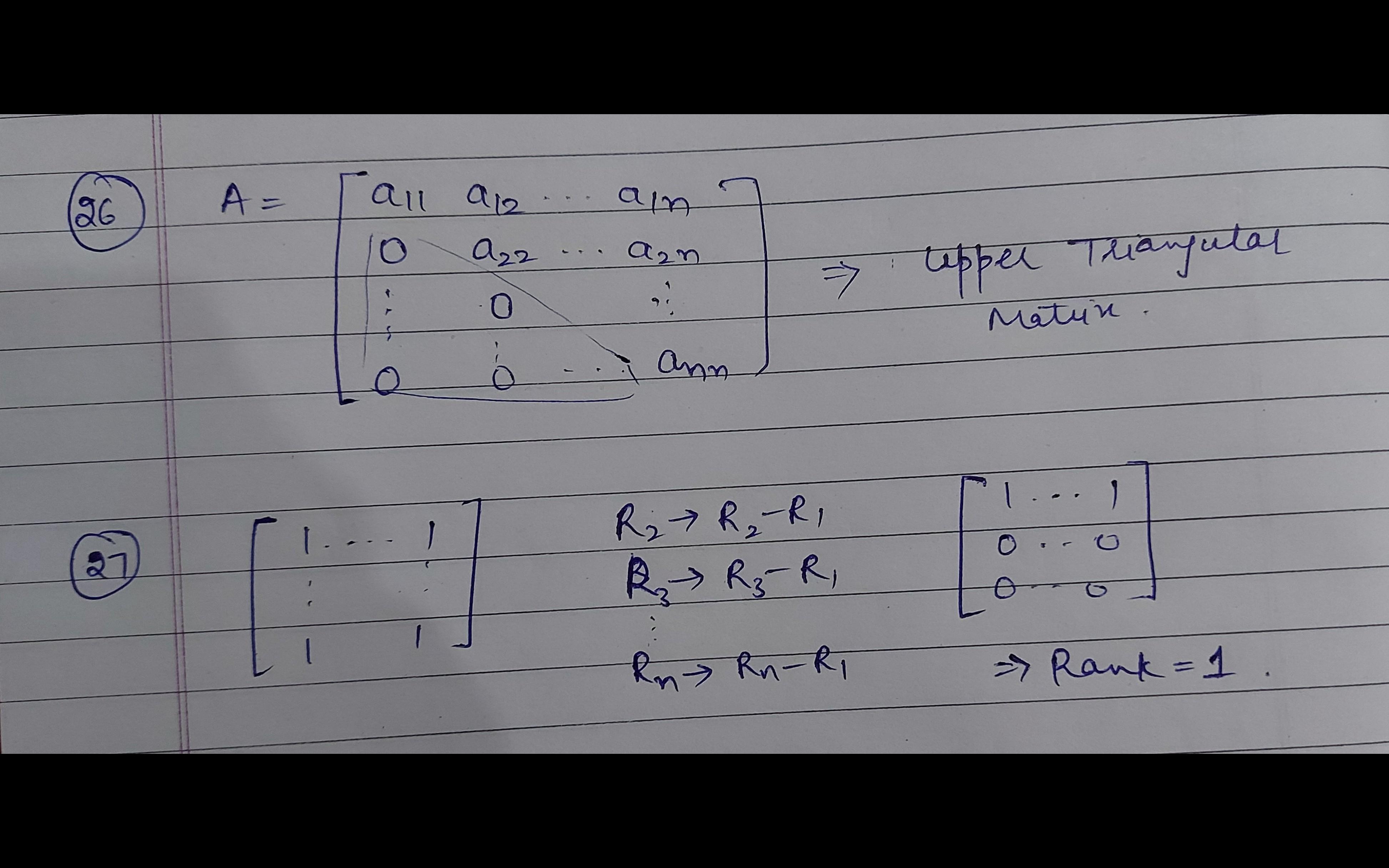
Please give me solutions and correct options for these questions :- 26,27,28,29,30,31,32.

1.26. A square matrix A in which the element dy=0 for i>jis called i) diagonal matrix (ii) lower triangular matrix The matrix Cos6 sin Cis (-sin 0 cos 0) () symmetric (ii) skew-symmetric (11) orthogonal (iv) singular Scanned with CamScanner (ii) upper triangular matrix (iv) null matrix -1 1.32. The 3 x 3 real matrix A=| | - 0 b 1,27. If a,=1 for all i, j then rank (A) is )1 (i) 0 (ii) number of rows of A (iv) number of columns of A is invertible if and only if () a=b=c (ii) a = b=c+0 (iv) a+b+c#00 (i) a = b=c=0 1.33. Let A be a nipolent 2 x2 square matri of index 10. Then (i) A = 0 (i) rank A=l (ii) A^ = (iv) rank A =2 2-1 0 1.28. The matrix- I 3 issimilar to the 134, If A. B, C are three n x n non-singular matrix B matrices, then rank oto c) (10 0 0 3 0 o 0 4) -21 I (1) atleast rank A + rank C (i) rank A + rank B + rank C (ii) rank A+ rank C (iv) rank A 21 1) (ii) -3| (iv) none of these 1.35. The rank of the real matrix (0-3-5 3 3 3 A= |3 3 3is 1.29. Which one of the following matrices is Hermitian ? 3 i)1 (i) 2 (ii)3 (iv)0 3 1.36. For an m x n matrix A with m S n, we always have () rank A sm (in) m S rank A Sn (ii) n S rank A (iv) m S rank A Sm+n I.30. Let P be a matrix of order m xn and Q be a matrix of order n x p, n # p. If| rank P =n and rank Q= p, then rank (PQ) is (5 0 0) 5 1.37. Let A =|1 0. Then for which X| )n i)p ii) np (iv) n+p o 5 there exists a scalar 7 such tna AX = Ax. 131. Consider a 2 x2 matrix A = | Ifa+d=1= ad - bc, then A equals )0 Gi)-h (ii) 312 Giv) l2 x-