IIT JAM
profile-img
Aditi agrawal Asked a Question
June 27, 2020 10:16 ampts 30 pts
  • IIT JAM
  • Physics (PH)

Please solve this question...

Problem 1.14 Suppose that f is a function of two variables (y and z) only. Show that the gradient Vf = (af/0y)ý +(0f/8z)2 transforms as a vector un- der rotations, Eq. 1.29. [Hint: (af/8y) = (8f/8y)(8y/8y) + (0f/az)(8z/0y), and the analogous formula for df/8z. We know that y= y cos o+ z sin ộ and Z=-y sino+zcos p; "solve" these equations for y and z (as functions of y and Z), and compute the needed derivatives 3y/8y, 3z/0y, ctc.]
  • 3 Answer(s)
Answer Now
  • 0 Likes
  • 5 Comments
  • Shares
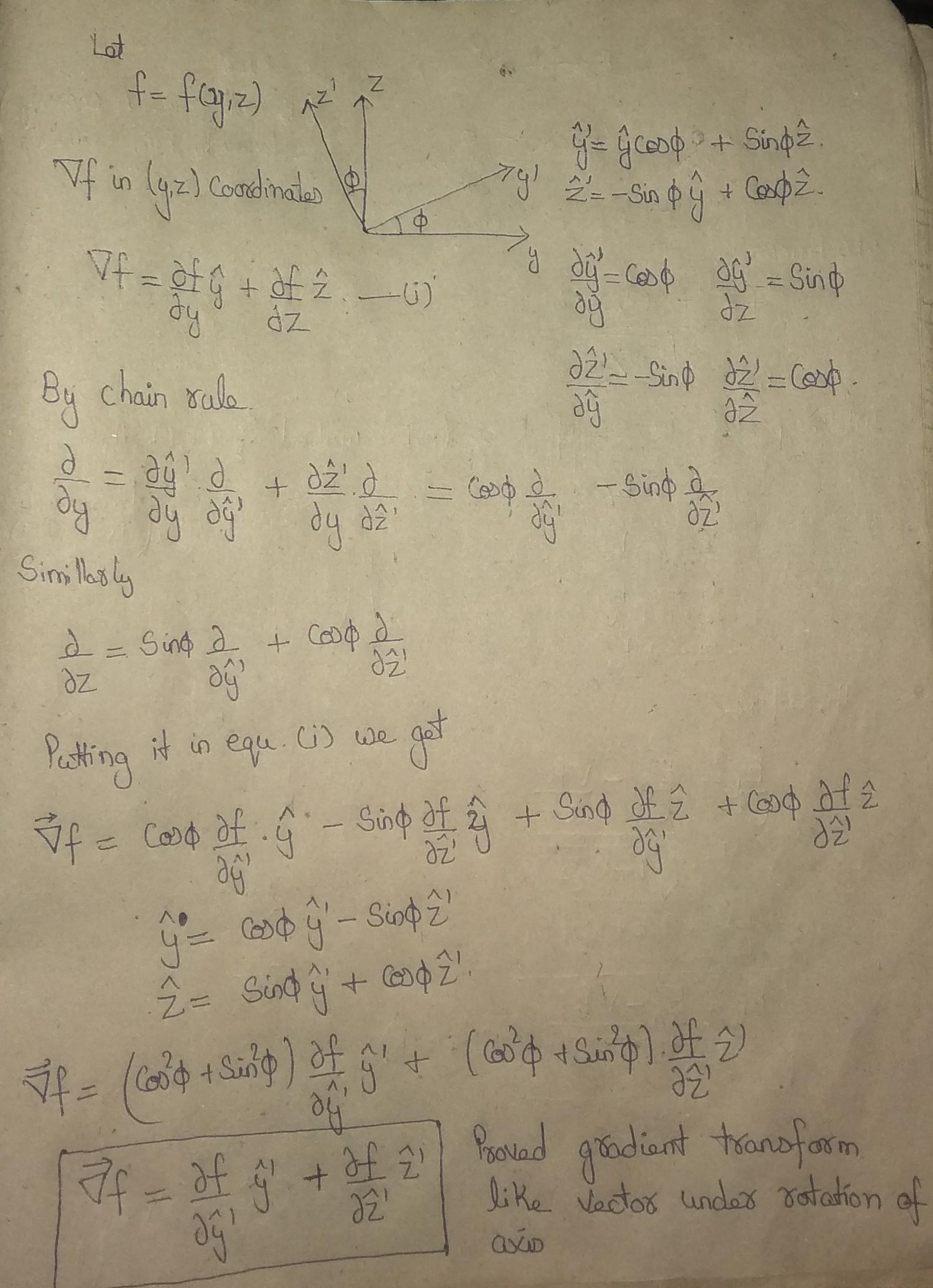
  • Ghost.
    Statement of Question- del(f) is a vector quantity so you have to prove it transform in a similar manners as a normal vector when axis are rotated by certain angle. i.e if del(f) i...
    Show more
    Likes(0) Reply(2)
    Aditi agrawal
    got ur point
  • Ghost.
    here i have attached the file, you can write the transformation into matrix form as well and operate on components of function.
    • cropped1606407907.jpg
    Likes(0) Reply(1)
    Aditi agrawal
    thank you very much
  • Ruby negi thankyou
    y bar and z bar
    • cropped-1972795523.jpg
    Likes(1) Reply(5)
    Aditi agrawal
    what does y bar represent
  • Ruby negi thankyou
    see ....
    • cropped751611214.jpg
    Likes(1) Reply(4)
    Aditi agrawal
    also please explain that what does question says
  • Ruby negi Best Answer
    see this solution.. for any help do let me know...
    • cropped1037121909.jpg
    Likes(1) Reply(5)
    Aditi agrawal
    how does thus ybar and z bar came.. can you please provide its derivation