IIT JAM
   Top Resources
Abhishek Patel posted an Question
April 22, 2023 • 17:20 pm 30 points
  • IIT JAM
  • Physics (PH)

Question 57 when laser light of wavelength falls on a metal scale with 1 mm engravings at a grazing angle of incidence, it is diffracted to form a vertical chai

Question 57 When laser light of wavelength falls on a metal scale with 1 mm engravings at a grazing angle of incidence, it is diffracted to form a vertical chain of diffraction spots on a screen kept perpendicular to the scale. If the wavelength of the laser is increased by 200 nm, the angle of the first order diffraction spot changes from 5° to (in degree) a. 6.60 b. 5.14 C. 5.018 d. 5.21

0 Answer(s) Answer Now
  • 0 Likes
  • 2 Comments
  • 0 Shares
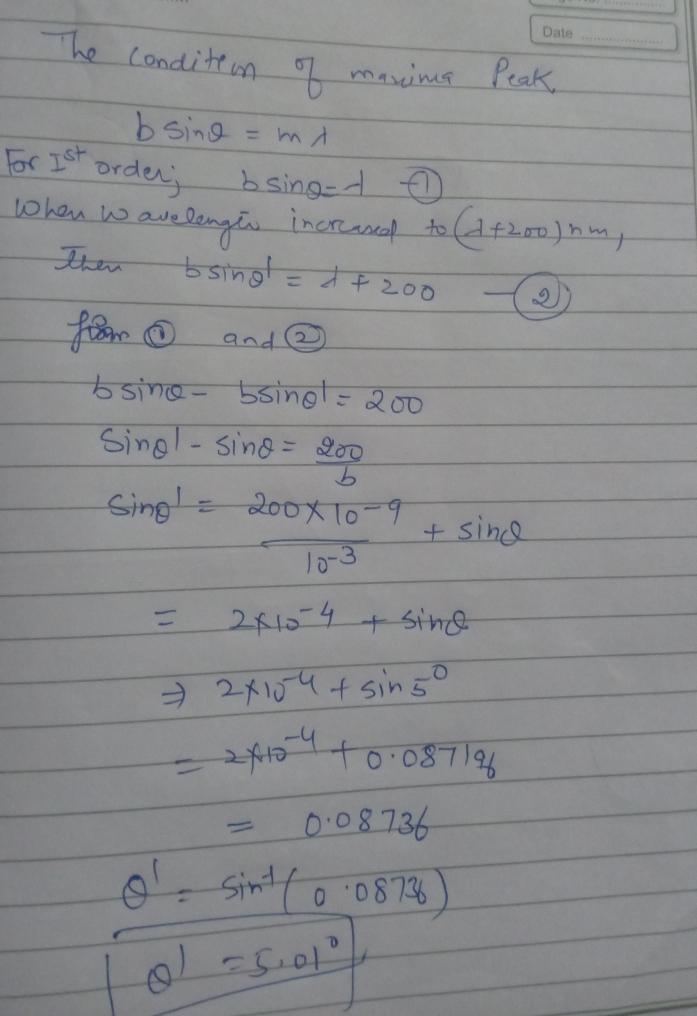
  • 7863939478

    To solve this problem, we can use the formula for the angle of diffraction for a grating: sinθ = mλ/d where: θ is the angle of diffraction, m is the order of the diffraction spot, λ is the wavelength of the incident light, and d is the spacing between the grating lines. Given information: The laser light falls on a metal scale with 1 mm engravings, which means the spacing between the grating lines (d) is 1 mm = 0.001 m. The angle of the first-order diffraction spot for the initial wavelength is 5°. Let's calculate the initial wavelength (λ1) using the given information. sinθ = mλ1/d sin(5°) = 1 * λ1 / 0.001 Rearranging the equation: λ1 = sin(5°) * 0.001 Now, we need to find the final wavelength (λ2) when the initial wavelength is increased by 200 nm (200 nm = 0.2 μm = 0.0002 mm). λ2 = λ1 + 0.0002 Now, we can calculate the new angle of the first-order diffraction spot (θ2) using the formula mentioned above. sinθ2 = mλ2/d sinθ2 = 1 * λ2 / 0.001 Let's substitute the values: sinθ2 = (λ1 + 0.0002) / 0.001 Now, we can solve for sinθ2: sinθ2 = (sin(5°) * 0.001 + 0.0002) / 0.001 Using a calculator, we find: sinθ2 ≈ 0.087463 Finally, we can find the angle θ2 by taking the inverse sine (sin^(-1)) of sinθ2: θ2 ≈ sin^(-1)(0.087463) Using a calculator, we find: θ2 ≈ 5.018° Therefore, the angle of the first-order diffraction spot changes to approximately 5.018°. So, the correct answer is option C. 5.018

whatsapp-btn

Do You Want Better RANK in Your Exam?

Start Your Preparations with Eduncle’s FREE Study Material

  • Updated Syllabus, Paper Pattern & Full Exam Details
  • Sample Theory of Most Important Topic
  • Model Test Paper with Detailed Solutions
  • Last 5 Years Question Papers & Answers

Sign Up to Download FREE Study Material Worth Rs. 500/-