
Greetings Knowledge Seekers!
Eduncle has come up with series for Number System tricks to edify Quantitative Aptitude and Logical Reasoning in an interesting manner.
This series will up-skill you with the QA and LR knowledge and also enhance your speed and accuracy to attempt more questions in minimal time.
The amazing short tricks and methods for solving Maths Number System questions are discussed below.
Here in this blog, we would discuss 4 important and simple rules to solve Number System questions during the exam.
These are –
Number System Divisibility Test
Number System Division & Remainder Rules
To refine your knowledge, We have also provided -
Number System Questions asked in Competitive Exams
Number System in Quantitative Aptitude - Types of Numbers
Below you can check the types of numbers in Maths along with their definitions and get edified well!
Natural Numbers – All positive or non-negative counting numbers. The set of natural numbers are commonly denoted as N.
Example - (1, 2, 3,4…..∞).

Whole Numbers – If we add zero in natural numbers set then it becomes whole numbers set.
Example - (0, 1, 2, 3,4…..∞).

Integers – Integers are all whole numbers which include negative numbers as well as positive numbers.
Example - (∞......-4,-3,-2,-1,0,1,2,3,4,5....∞).

Even & Odd Numbers – If the number is divided by 2 then it is called even number and if it is not then the numbers are called odd numbers.
Example - (0,2,4,6,8,10,12.....∞) are even numbers and (1,3,5,7,9,11,13,15,17,19....∞) are odd numbers.
Prime Numbers – If a number is divided by itself only then it is called prime number. Prime Numbers can be positive or negative except 1.
Example - (2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61....∞)
Composite Numbers – Natural numbers which are not prime are called composite numbers.
Example – (4,6,8,9,10,12,14,15,16,18,20,21,22,……….. ∞)

Co-Prime Numbers - Two natural number a and b are said to be co-prime if their HCF is 1.
In a simpler way, two integers (a and b) are coprime (or relatively prime) if they share no common factors. In other words, there is no number, other than 1, that divides both a and b evenly.
Example - 6 and 35 are coprime, because the factors of 6, 2 and 3, do not divide 35 evenly. 6 and 27 are not coprime, because 3 divides both 6 and 27.
Number System in Quantitative Aptitude - Divisibility Test
Know the shortcuts for Number System Divisibility Test by scrolling down.
| Divisible by 2 – If a number ends with 0,2,4,6,8 then the number is divisible by 2. Example – 254, 326, 3548, 4210. All number ends with 4,6,8,0 so these numbers are divisible by 2.
|
| Divisible by 3 - If sum of all the digits of a number is divisible by 3, then the number itself, is also divisible by 3. Example – 375,4251,78123. Here we are taking another example of 549 – 5+4+9 = 18 which is divisible by 3, so 549 is also divisible by 3.
|
| Divisible by 4 – If the last two digits of any number is divisible by 4, then the number is also divisible by 4. Example – 2348.Here last two digits 48 are divisible by 4, so 2348 is also divisible by 4.
|
| Divisible by 5 – If a number ends with 0 or 5, then it is divisible by 5. Example – 340, 625.
|
| Divisible by 6 – If a number is divisible by both 2 and 3, then it is divisible by 6 as well. Example – 4536. Here the number ends on 6 which is divisible by 2 and the sum of digits (4+5+3+6 = 18) which is divisible by 3 also, so the number 4536 is divisible by 6.
|
| Divisible by 8 – If the last three digits of a number can be divided by 8, then the number is divisible by 8. Example – 746848. Here last 3 digits 848 are divided by 8, hence the number 746848 is divisible by 8.
|
| Divisible by 10 – If a number ends with 0, then it is divisible by 10.
Example – 120, 330, 500.
|
| Divisible by 11 – If (sum of its digit in odd places) is subtracted by (sum of its digits in even places) = 0 or multiple of 11, then the number is divisible by 11. Example – 39798846Sum of digits at odd places = 3+7+8+4 = 22 Sum of digits at even places = 9+9+9+6 = 33Now -> 33-22 = 11 which is multiple of 11 so number is divisible.
|
| Divisible by 12 – If a number is divisible by 3 and 4 both, then it will also be divisible by 12 as well. Example – 4848 is divisible by 3 and 4 both, so it will be divisible by 12 also.
|
| Divisible by 14 – If a number is divisible by 2 and 7 both, then it will also be divisible by 14 as well. Example – 4242 is divisible by 2 and 7 both, so it will be divisible by 14 also.
|
| Divisible by 15 – If a number is divisible by 3 and 5 both, then it will also be divisible by 15 as well. Example – 4545 is divisible by 3 and 5 both, so it will be divisible by 15 also.
|
| Divisible by 16 – A number is divisible by 16, if the number formed by the last4 digits is divisible by 16.
Example - 7957536 Last four digits 7536 are divisible by 16.
|
| Divisible by 24 – If a number is divisible by 3 and 8 both, then it will also be divisible by 14 as well. Example – 4848 is divisible by 3 and 8 both, so it will be divisible by 24 also.
|
| Divisible by 40 – If a number is divisible by 5 and 8 both, then it will also be divisible by 40 as well. Example – 8080 is divisible by 5 and 8 both, so it will be divisible by 40 also.
|
| Divisible by 80 – If a number is divisible by 5 and 16 both, then it will also be divisible by 80 as well. Example – 80160 is divisible by 5 and 16 both, so it will be divisible by 80 also.
|
Number System PDF in Quantitative Aptitude – Division and Remainder Rules
As per the Number Systems’ Division and Remainder Rules, we have to divide an integer (dividend) with another integer (divisor) and get the quotient and remainder values.
Eduncle has come up with the easiest method of solving long division calculations.
Example – Here we take 487 as dividend and 32 as divisor. Now we have to find out the quotient and remainder.
Let’s have a look!
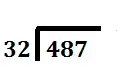 |
We set up our problem with the long division symbol or the long division bracket. Put the dividend on the inside and the divisor on the outside, left. | |
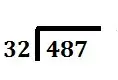 |
Divide the first number of the dividend by the divisor.You can note the remainder but ignore it for now. | 4 ÷ 32 = 0 with a remainder of 4 |
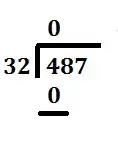 |
The whole number result, 0, is placed on top to start the quotient. That number is then multiplied by the divisor.The result is placed under the number we just divided into. | 32 * 0 = 0 |
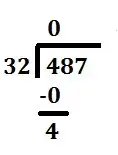 |
Next, subtract the bottom number from the top. | 4 - 0 = 4 |
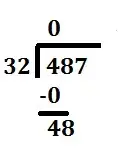 |
Next, we bring down the next number of the dividend. | 48 |
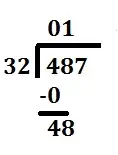 |
We now divide this number (48) by the divisor (32). Again, You can note the remainder but ignore it for now.Note that you could skip all of the previous steps with zeros and jump straight to this one if you realize how many digits in the dividend you need to get your first non-zero value in the quotient. In this case you would divide 32 into 48 straight away. | 48 ÷ 32 = 1 with a remainder of 16 |
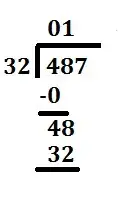 |
The whole number result (1) of this equation is placed in the second position of the quotient. Like the first go around, we then multiply that number by the divisor. Again, the result is placed under the number divided into.
|
32 * 1 = 32 |
 |
Subtract the product, 32, from the number above it. | 48 - 32 = 16 |
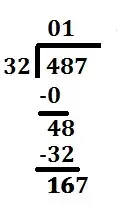 |
Bring down the next number from the dividend. | 167 |
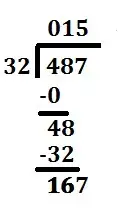 |
Divide this number (167) by the divisor (32). See a pattern emerging? | 167 ÷ 32 = 5 with a remainder of 7 |
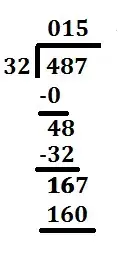 |
The whole number result (5) of this equation is placed in the next position of the quotient. Just like before, multiply that number by the divisor.Again, the result is placed under the number divided into. | 32 * 5 = 160 |
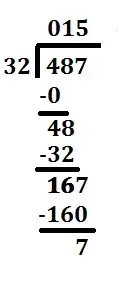 |
Subtract the result from the number above | 167 - 160 = 7 |
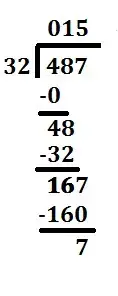 |
As this is the last number, the amount left over (7) is the remainder and the quotient is 15. We're all done. | 487 ÷ 32 = 15 with a remainder of 7 |
15 is the quotient and 7 is the remainder.
In case we have given with the quotient or remainder and have to find out the values of dividend or divisor, then we can use the formula given below-
“Dividend = (Divisor * Quotient) + Remainder Or x = kq + r”
Number System in Maths (Quantitative Aptitude) – Sum Rules
Here we’ll be discussing the basic formulas of Arithmetic Progression and Geometrical Progression.
Arithmetic Progression
If An A.P. with first term a and common difference d is given as-
a, (a+d), (a+2d), (a+3d), ..... a, (a+d), (a+2d), (a+3d) ,.....
Then the formula to calculate its nth term will be – Tn = a + (n−1) * d.
The sum of n terms of this A.P.
Sn = (n2) * [2a +(n − 1) * d]Sn = (n2) ∗ (first term + last term).
Also practice with -
(1+2+3+.........+n) = ½ * n * (n+1)
(12+22+32+.........+n2) = 1/6 * n * (n+1) * (2n+1)
(13+23+33+.........+n3) = 1/4 * n2 * (n+1) * 2.
Geometric Progression
A G.P. with first term a and common ratio r is –
a, ar, ar2, ..... : a, ar, ar2, .....
In this G.P. nth term = Tn = a*r(n−1)
Sum of n terms=
Sn = a * (1−rn) / (1−r)Sn = a * (1−rn) / (1−r); when r>1.
Number System Formulas – Learn the Basics!

Sample Maths Number System Questions – FAQ’s!
Type-1: Given a number x, you will be asked to find the largest n digit number divisible by x.
Type-2: You will be given with a set of numbers (n1, n2, n3...) and asked to find how many of those numbers are divisible by a specified number x.
Type-3: Given a number series, find the sum of n terms, find nth term etc.
Type-4: Find product of two numbers when their sum/difference and sum of their squares is given.
Type-5: Find the number when divisibility of its digits with certain numbers is given.
Type-6: Find the smallest n digit number divisible by x.
Type-7: Which of the given numbers are prime numbers.
Type-8: Number x when divided by y gives remainder r, what will be the remainder when x2 is divided by y.
Type-9: Given relationship between the digits of number, find the number.
Type-10: Find result of operations (additions, subtractions, multiplications, divisions etc.) on given integers. These integers can be large and the question may look difficult and time consuming. But mostly the question will map onto one of the known algebraic equations given in this first tab.
Suggested Reads -
Know about IBPS PO In detail. Please visit - IBPS PO Exam | Recruitment Updates & Notifications.
Stay updated with every single detail about IBPS Clerk. Please visit - IBPS Clerk Recruitment Exam (Prelim |Mains) Notifications.
Fulfill your dream of becoming IBPS SO. Please visit - IBPS Specialist Officers | IT Officers Recruitment Exam.
Begin your preparation for IBPS RRB now!. Please visit - IBPS RRB Recruitment Exam | Updates & Notifications.
Hope the above information will help you in learning the short tricks and practicing number system with given formulas.
For more topics, Stay tuned with Eduncle!


















