Matrices and Determinants is a very important topic in Mathematics. Although it is taught to students from 12th to Graduation Level, in this article we'll provide you step by step lessons, MCQs and Numerical of IIT JAM Exam (M.Sc.). Get Eduncle's study notes with formulas, questions and solutions to know what are Matrix and Determinant and how to solve these questions.
Download Free PDF for Matrix and Determinants:
In this brain-friendly guide, you'll study and quickly grasp the following concepts:
1. Introduction - What are Matrix and Determinants?
2. Matrix and Determinant (All Formulas)
3. Theory
Basic Level Questions (3 Questions)
Challenging Questions (3 Questions)
Question asked in IIT JAM from Matrix and Determinant (5 Questions)
5. Related topics to be studied before reading Matrix and Determinant.
So, load your brain with these important concepts! After completing all the topics, try solving the following questions and you will easily score full marks from this unit. Answers to these questions are given in the end. You can verify your answers and check your level of understanding.
What Are Matrix and Determinants? - Introduction
The knowledge of matrices and determinants applies to several branches of science, as well as different mathematical disciplines. Matrices are one of the most powerful tools in mathematics. It simplifies our work to a great extent when compared with other direct methods. The transformation of the concept of matrices results in obtaining compact and simple methods of solving systems of linear equations.
Applications:
We use Matrices not only for the representation of the coefficients in a system of linear equations but it’s using far exceeds.
The notation and operations of Matrices are used in electronic spreadsheet programs for personal computer, which can be further used in different areas of business and science like budgeting, sales projection, cost estimation, analyzing the results of an experiment etc.
Also, many physical operations such as magnification, rotation and reflection through a plane can be represented mathematically by matrices.
Matrices are also used in cryptography.
This mathematical tool is not only used in certain branches of sciences, but also in genetics, economics, sociology, modern psychology, and industrial management.
For IIT JAM this topic is comparatively easy and scoring. If you want to get this theory lesson in PDF format, then hit the download button below:
Download IIT JAM 2021 Notes & Theory for Free
Matrix and Determinants (All Formulas)
Any matrix A and its transpose both have the same Eigen values.
The trace of the matrix equals the sum of the Eigen values of a matrix.
The determinant of the matrix A equals to the product of the Eigen values of A.
If λ1, λ2, ....., λn are the n-Eigen values of A, then
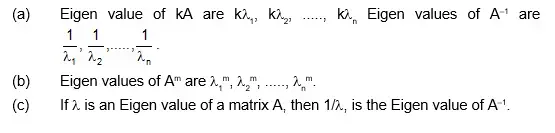
Cayley Hamilton Theorem
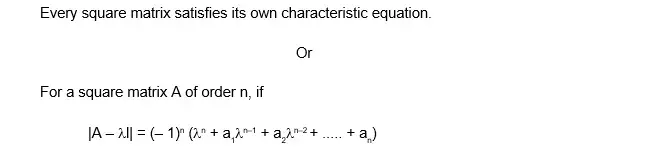
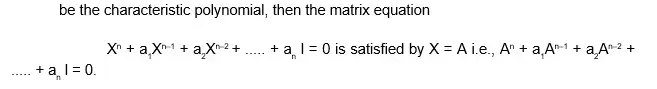
A be an nxn matrix and let

Matrix exponential for a square matrix A,
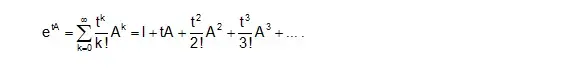
Download IIT JAM Previous Papers & Answers for Free
Description
A matrix (plural matrices) is an ordered rectangular table of elements (or entries). The numbers or functions are called the elements or the entries of the matrix.
We denote matrices by capital letters.
For example:
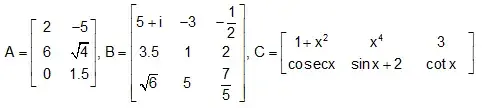
In the above examples, the horizontal lines of elements are called rows of the matrix and the vertical lines of elements are called columns of the matrix. Thus A has 3 rows and 2 columns, B has 3 rows and 3 columns while C has 2 rows and 3 columns.
Order of a matrix
A matrix having m rows and n columns is called a matrix of order m × n or simply m × n matrix (read as an m by n matrix). So referring to the above examples of matrices, we have A as 3 × 2 matrix, B as 3 × 3 matrix and C as 2 × 3 matrix. We observe that A has 3 × 2 = 6 elements, B and C have 9 and 6 elements, respectively.
In general, an m × n matrix has the following rectangular array:

or A = [aij]m×n, 1 ≤ i ≤ m, 1 ≤ j ≤ n i, j ∈ N
Thus the ith row consists of the elements ai1, ai2, ai3, ..., ain, while the jth column consists of the elements a1j, a2j, a3j, ..., amj,
In general aij, is an element lying in the ith row and jth column. We can also read it as the (i, j)th element of A. The number of elements in an m × n matrix will be equal to mn.
Determinant
To every square matrix A = [aij] of order n, we can associate a number (real or complex) called determinant of the matrix A, written as det A, where aij is the (i, j)th element of A.

NOTE:
(i) Only square matrices have determinants.
(ii) For a matrix A, |A| is called determinant of A and not modulus of A.
Determinant of a Matrix of Order One
Let A = [a] be the matrix of order 1, then the determinant of A is defined to be equal to a.
Determinant of a Matrix of Order Two

Determinant of a Matrix of Order Three
The determinant of a matrix of order three can be determined by expressing it in terms of second-order determinants which is known as expansion of determinant along a row (or a column). There are six ways of expanding a determinant of order 3 corresponding to each of three rows (R1, R2 and R3) and three columns (C1, C2 and C3) and each way gives the same value.
Consider the determinant of a square matrix A = [aij]3×3, i.e.

Eigen values and Eigen vectors
Definitions:
Let A = [aij]n×n be a square matrix of order n, I is an unit matrix of order n and λ an indeterminate, then the matrix.

Also the equation |A – λ| = 0, is called the characteristic equation of A. The roots of this equations are called the characteristic roots or characteristic value or Eigen roots or Eigen values of latent roots of the matrix.
The set of the Eigen values of the matrix A is called the spectrum of the matrix A. If λ is a characteristic root of a n × n matrix A, then the non-zero solution
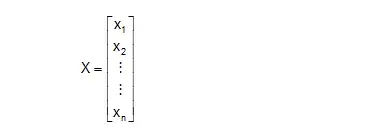
of the equation A X = λ X i.e. (A – λ|) X = 0 is called the characteristic vector or Eigen vector of the matrix A corresponding to the characteristic root λ.
Chief Characteristics of Eigen Values:
The sum of the elements of the principal diagonal of a matrix is called the trace of the matrix.
(i) Any matrix A and its transpose both have the same Eigen values.
(ii) The trace of the matrix equals to the sum of the Eigen values of a matrix.
(iii) The determinant of the matrix A equals to the product of the Eigen values of A.
(iv) If λ1, λ2, ....., λn are the n-Eigen values of A, then
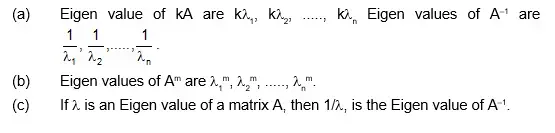
Some important Theorems




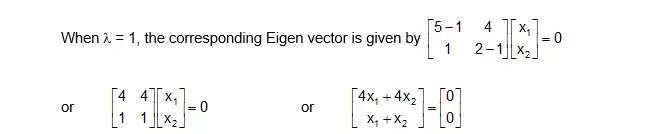

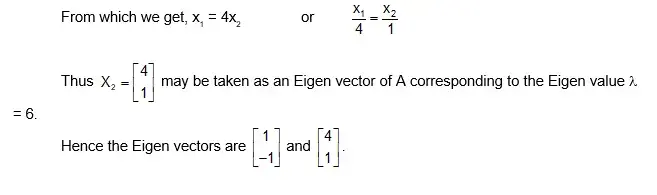
Liked what you read? Download the PDF copy for free to master concepts of eigen value and vectors here:
Download IIT JAM Sample Study Material Free PDF
Cayley Hamilton Theorem
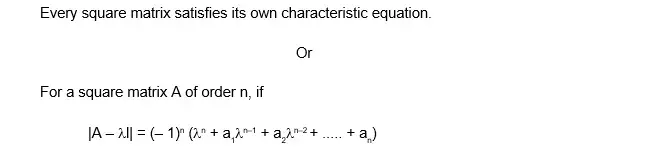
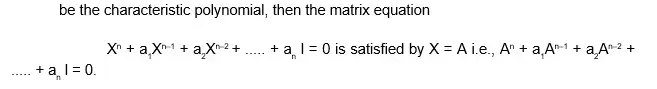
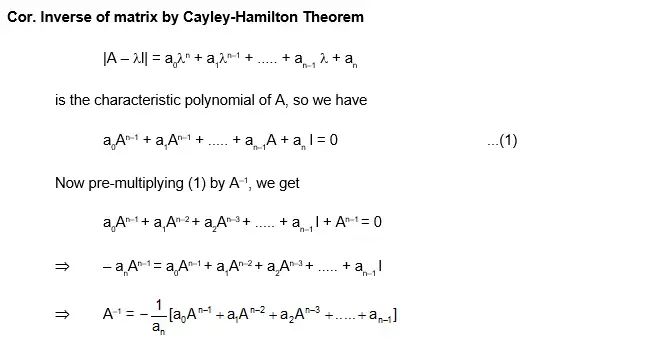



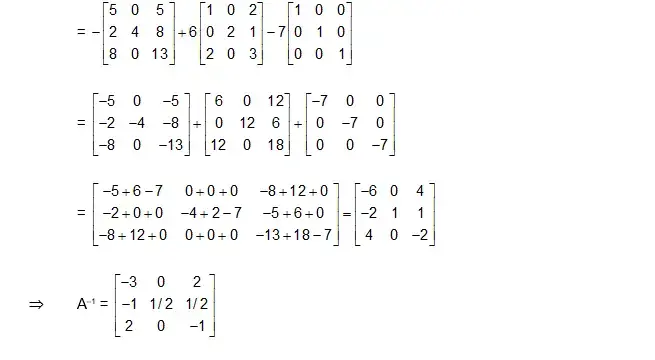
Practice Questions for Matrix and Determinants
Download the Practice Question PDF for Matrix and Determinants and get the solutions for all the below mentioned questions.
Download Free IIT JAM Model Papers PDF
Basic Level Questions on Matrix and Determinant

Multiple Selection Question


Numerical Type Question
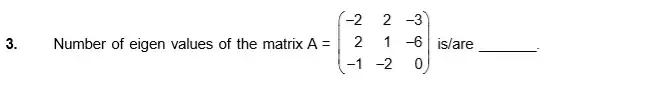
Challenging Questions on Matrix and Determinant
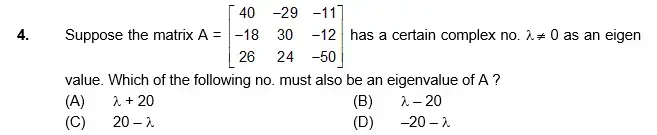
Numerical Type Question

Multiple Selection Question

Previous Year Questions on Matrix and Determinant

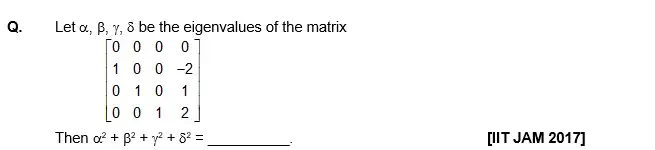
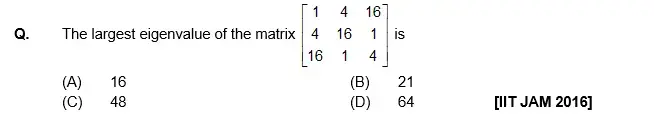



Related Topics:
Matrix and operations
Inverse of Matrix
Trace of a Matrix
Determinant
Minimal Polynomial
Type of Matrices
Algebraic and geometric multiplicity.
FAQ About Matrix and Determinants:
What is the difference between matrix and determinants?
Key Difference: A matrix or matrices is a rectangular grid of numbers or symbols that is represented in a row and column format. A determinant is a component of a square matrix and it cannot be found in any other type of matrix.
Who invented matrix and determinants? Carl Gauss (1777-1855), the greatest German mathematician of the 19th century, first used the term 'determinant' in 1801. Matrices began in the 2nd century BC with the Chinese although traces could be seen back in the 4th century BC with the Babylonians. It was only towards the end of the 17th century that much progress was made on the studies of matrices.
Hope we have provided you detailed information about Matrix and Determinants. Comment us in the below section for any query.























